题目内容
2．已知△ABC中，AB=AC，AB的垂直平分线交AC于D，△ABC和△DBC的周长分别是30cm和19cm，则△ABC的腰和底边长分别为（ ）| A． | 11cm和8cm | B． | 8cm和11cm | C． | 10cm和8cm | D． | 12cm和6cm |
分析 根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，然后求出△DBC的周长=AC+BC，再根据两个三角形的周长求出AB，然后BC的值，从而得解．
解答 解：∵AB的垂直平分线交AC于D，
∴AD=BD，
∴△DBC的周长=BD+CD+BC=AD+CD+BC=AC+BC，
∵△ABC和△DBC的周长分别是30cm和19cm，
∴AB=30-19=11cm，
∴BC=19-11=8cm，
即△ABC的腰和底边长分别为11cm和8cm．
故选A．
点评 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，三角形的周长，熟记性质并准确识图是解题的关键．
练习册系列答案
相关题目
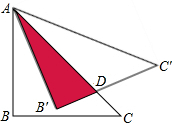如图，等腰直角三角形ABC的直角边AB的长为6cm，将△ABC绕点A逆时针旋转一定角度α（α为锐角）后得到△AB′C′．使得B′C′交AC边于点D，点D不与点B′重合，则有下列结论：①∠ADB′=45°+α；②∠α＜45°；③若AD的长为整数，则AD等于7cm；④当α=15°时，阴影部分的面积为6$\sqrt{3}$cm2．其中正确结论的序号是①②④（把所有正确的序号都填在横线上）
13．下列运算正确的是（ ）
| A． | $\sqrt{9}÷\sqrt{3}$=3 | B． | $\sqrt{6}+\sqrt{2}=\sqrt{8}$ | C． | $\sqrt{{{（-5）}^2}}$=-5 | D． | $\sqrt{\frac{1}{2}}×\sqrt{8}$=2 |
10．一组数据1，2，3，5，4，3中的中位数和众数分别是（ ）
| A． | 3，3 | B． | 5，3 | C． | 4，3 | D． | 5，10 |
11．
如图，在?ABCD中，AB=4，BC=7，∠ABC的平分线交AD于点E，则DE的长为（ ）
如图，在?ABCD中，AB=4，BC=7，∠ABC的平分线交AD于点E，则DE的长为（ ）| A． | 5 | B． | 4 | C． | 3 | D． | 2 |