题目内容
19.证明:过三角形一边中点与另一边平行的直线必平分第三边.分析 根据平行四边形的判定与性质,可得BD与CF的关系,根据平行线的性质,可得内错角相等,再根据全等三角形的判定与性质,可得答案.
解答 已知:D是AB的中点,DE∥BC,求证:AE=CE.
证明:如图延长DE至F点使DF=BC,连接CF ,
,
∵DF∥BC,DF=BC,
∴四边形BCFD是平行四边形,
∴BD=CF,BD∥CF,
∴∠ADE=∠EFC,∠A=∠FCE.
∵D是AB的中点,
∴AD=BD,
CF=AD.
在△ADE和△CFE中,
$\left\{\begin{array}{l}{∠A=∠FCE}\\{AD=CF}\\{∠ADE=∠CFE}\end{array}\right.$,
∴△ADE≌△CFE (ASA),
∴AE=CE.
点评 本题考查了三角形中位线定理,利用了平行四边形的判定与性质,全等三角形的判定与性质.

练习册系列答案
相关题目
4.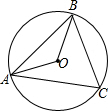 如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )
如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )
 如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )
如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )| A. | 50$\sqrt{3}$ | B. | $\frac{100}{3}$$\sqrt{3}$ | C. | $\frac{200}{3}$$\sqrt{3}$ | D. | 200$\sqrt{3}$ |
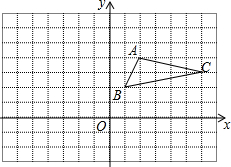 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.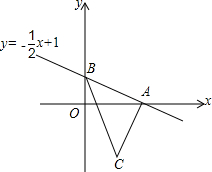 如图,已知直线y=-$\frac{1}{2}$x+1与坐标轴交于A、B两点,C(1,-2),点P在y轴的负半轴上,且S△PAB=S△ABC.
如图,已知直线y=-$\frac{1}{2}$x+1与坐标轴交于A、B两点,C(1,-2),点P在y轴的负半轴上,且S△PAB=S△ABC.
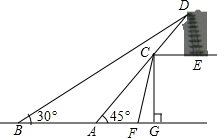 如图为某风景区中古塔,大坝和湖的截面图,大坝顶端CE和水面平行,点C为大坝顶端拐角处,大坝的坡比i=3:1(即CG:FG=3:1),当小明和同伴从大坝的点F处沿着截面所在方向开始划船,划行20米到达点A处时,他们以仰角45°观察远方,正好看到古塔顶端的点D,且点C在视线AD上,当他们从点A继续沿原方向划船40米,到达点B处时,观察点D的仰角正好为30°.
如图为某风景区中古塔,大坝和湖的截面图,大坝顶端CE和水面平行,点C为大坝顶端拐角处,大坝的坡比i=3:1(即CG:FG=3:1),当小明和同伴从大坝的点F处沿着截面所在方向开始划船,划行20米到达点A处时,他们以仰角45°观察远方,正好看到古塔顶端的点D,且点C在视线AD上,当他们从点A继续沿原方向划船40米,到达点B处时,观察点D的仰角正好为30°.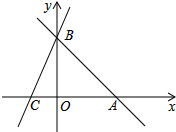 直线CB:y=3x+b分别与x,y轴交于C(-2,0),B两点,过点B的直线交x轴正半轴于点A,且OB=OA.
直线CB:y=3x+b分别与x,y轴交于C(-2,0),B两点,过点B的直线交x轴正半轴于点A,且OB=OA.