题目内容
9.先化简,再求值:($\frac{6}{{x}^{2}-9}$-$\frac{1}{x-3}$)•$\frac{3+x}{x}$,其中x=2.分析 先根据实数混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{6-(x+3)}{(x+3)(x-3)}$•$\frac{3+x}{x}$
=$\frac{-(x-3)}{(x+3)(x-3)}$•$\frac{3+x}{x}$
=-$\frac{1}{x}$,
当x=2时,原式=-$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
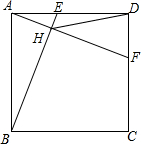 如图,E,F是正方形ABCD边AD,CD上两个动点,且AE=DF,BE交AF于H,AB=2,连接DH.
如图,E,F是正方形ABCD边AD,CD上两个动点,且AE=DF,BE交AF于H,AB=2,连接DH.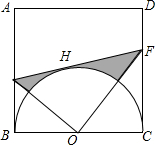 如图,正方形ABCD的边长为2a,以BC为直径在正方形内作半圆O,H是该半圆上一点,过点H作半圆的切线交AB、CD于E、F.
如图,正方形ABCD的边长为2a,以BC为直径在正方形内作半圆O,H是该半圆上一点,过点H作半圆的切线交AB、CD于E、F.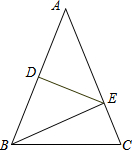 如图,己知△ABC,AB=AC,DE垂直平分AB,分别交AB、AC于D、E两点,若AB=12cm,BC=8cm,∠A=48°,求△BCE的周长和∠EBC的度数.
如图,己知△ABC,AB=AC,DE垂直平分AB,分别交AB、AC于D、E两点,若AB=12cm,BC=8cm,∠A=48°,求△BCE的周长和∠EBC的度数.