题目内容
4.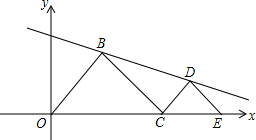 如图,E为(8,0),C是线段OE上一动点(不包括两个端点),分别以OC、CE为斜边,在第一象限作等腰Rt△OBC和等腰Rt△CDE,其中∠OBC=∠CDE=90°.设OC=a
如图,E为(8,0),C是线段OE上一动点(不包括两个端点),分别以OC、CE为斜边,在第一象限作等腰Rt△OBC和等腰Rt△CDE,其中∠OBC=∠CDE=90°.设OC=a(1)请表示B,D两点的坐标.(用含字母a的代数式表示);
(2)若OC:OE=3:1时,求直线BD的解析式;
(3)若两等腰直角三角形与一次函数y=-$\frac{1}{3}$x+3恰好有四个交点,求a的取值范围.
分析 (1)如图,过点B作BM⊥OC于M,过点D作DN⊥CE于N,则∠BMO=∠CND=90°,利用等腰三角形的性质求出OM=BM=$\frac{a}{2}$,CN=DN=$\frac{8-a}{2}$=4-$\frac{a}{2}$,ON=OC+CN=a+$\frac{8-a}{2}=4+\frac{a}{2}$,即可解答.
(2)求出B(3,3),D(7,1),利用待定系数法求出直线BD的解析式,即可解答.
(3)根据只要直线BD的B点、D点均在一次函数y=-$\frac{x}{3}$+3的上方时,则一次函数与直线BD就恰好有四个交点,得到-$\frac{1}{3}•\frac{a}{2}+3<\frac{a}{2}$ ①,-$\frac{1}{3}•(4+\frac{a}{2})+3<4-\frac{a}{2}$ ②,即可解答.
解答 解:(1)如图,过点B作BM⊥OC于M,过点D作DN⊥CE于N,
则∠BMO=∠CND=90°,
∵等腰Rt△OBC和等腰Rt△CDE,其中∠OBC=∠CDE=90°.
∴BM垂直平分OC,DN垂直平分CE,且Rt△BMO为等腰直角三角形,Rt△DNC为等腰直角三角形,
∵OC=a,E(8,0),
∴CE=8-a,
∴OM=BM=$\frac{a}{2}$,CN=DN=$\frac{8-a}{2}$=4-$\frac{a}{2}$,
∴ON=OC+CN=a+$\frac{8-a}{2}=4+\frac{a}{2}$,
∴B($\frac{a}{2},\frac{a}{2}$),D(4+$\frac{a}{2}$,4-$\frac{a}{2}$).
(2)若OC:CE=3:1,
∵OE=8,
∴OC=6,CE=2,
∴B(3,3),D(7,1),
设直线BD的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{3k+b=3}\\{7k+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{9}{2}}\end{array}\right.$.
∴直线BD的解析式为:y=-$\frac{1}{2}$x+$\frac{9}{2}$.
(3)一次函数y=-$\frac{x}{3}$+3,
∴该函数与x轴的交点P为(9,0),
该函数与x轴的交点Q为(0,3),
∴OQ=3,OP=9,
∴OP>OE,
∴只要直线BD的B点、D点均在一次函数y=-$\frac{x}{3}$+3的上方时,则一次函数与直线BD就恰好有四个交点,
由(1)得:B($\frac{a}{2},\frac{a}{2}$),D(4+$\frac{a}{2}$,4-$\frac{a}{2}$).
∴-$\frac{1}{3}•\frac{a}{2}+3<\frac{a}{2}$ ①
-$\frac{1}{3}•(4+\frac{a}{2})+3<4-\frac{a}{2}$ ②
由①得:a>$\frac{9}{2}$,
由②得:a<7,
∴$\frac{9}{2}$<a<7.
点评 本题考查了求一次函数的解析式、等腰直角三角形的性质,解决本题的关键是作出辅助线,结合图象进行解决问题.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案| A. | 互为相反数的两数均为一正一负 | B. | 1是最小的正整数 | ||
| C. | 有理数包含正有理数与负有理数 | D. | 一个数的绝对值是正数 |
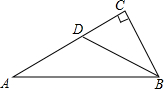 如图所示,在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,D是AC上一点,∠CBD=∠A,sin∠CDB=$\frac{2\sqrt{5}}{5}$.
如图所示,在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,D是AC上一点,∠CBD=∠A,sin∠CDB=$\frac{2\sqrt{5}}{5}$.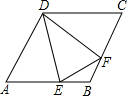 如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF.
如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF. 在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式.
在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式.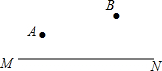 直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图)
直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图) 如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F.
如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F. 已知:如图,△ABC,BD=CD,AD平分∠BAC,求证:∠BAC+∠BDC=180°.
已知:如图,△ABC,BD=CD,AD平分∠BAC,求证:∠BAC+∠BDC=180°.