题目内容
14．
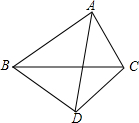已知：如图，△ABC，BD=CD，AD平分∠BAC，求证：∠BAC+∠BDC=180°．
分析 过D作DM⊥AB于M，DN⊥AC交AC的延长线于N，根据角平分线的性质得到DM=DN，推出Rt△BDM≌Rt△CDN，于是得到∠BDM=∠CDN，根据四边形的内角和得到∠BAC+∠MDN=180°，等量代换即可得到结论．
解答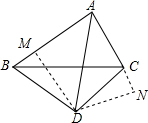 
证明：过D作DM⊥AB于M，DN⊥AC交AC的延长线于N，
∵AD平分∠BAC，
∴DM=DN，
在Rt△BDM与Rt△CDN中，$\left\{\begin{array}{l}{BD=CD}\\{DM=DN}\end{array}\right.$，
∴Rt△BDM≌Rt△CDN，
∴∠BDM=∠CDN，
∵∠AMD+∠AND=180°，
∴∠BAC+∠MDN=180°，
∴∠BDC+∠BAC=180°．
点评 本题考查了全等三角形的判定和性质，四边形的内角和，角平分线的性质，正确作出辅助线构造全等三角形是解题的关键．
练习册系列答案
单元加期末复习先锋大考卷系列答案
出彩同步大试卷系列答案
相关题目
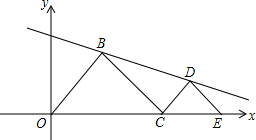如图，E为（8，0），C是线段OE上一动点（不包括两个端点），分别以OC、CE为斜边，在第一象限作等腰Rt△OBC和等腰Rt△CDE，其中∠OBC=∠CDE=90°．设OC=a
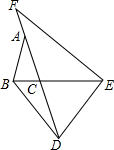如图，△ABC中，AB=AC，点D在AC的延长线上，点E在BC的延长线上，DB=DE，∠FAB+∠F=180°，求证：EF=AD．
2．已知从山脚起每升高100米，气温就下降0.6摄氏度，现测得山脚处的气温为14.1摄氏度，山上点P处的气温为11.1摄氏度，则点P距离山脚处的高度为（ ）
| A． | 50米 | B． | 200米 | C． | 500米 | D． | 600米 |
如图所示，要使图中平面展开图按虚线折叠成正方体后相对面上两个数之和相等，则b-c=-7．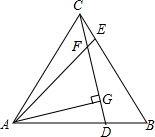
如图，等边三角形ABC中，DE分别是AB，BC边上的点，AD=BE，AE与CD相交于F，AG⊥CD，垂足为G，则sin∠AFG=$\frac{\sqrt{3}}{2}$．
3．以下计算正确的是（ ）
| A． | $\sqrt{2}+\sqrt{4}=\sqrt{6}$ | B． | $\root{3}{27}$=9 | C． | $\sqrt{{{（-3）}^2}}$=3 | D． | $（\sqrt{5}-\sqrt{2}）（\sqrt{5}+\sqrt{2}）$=10 |