题目内容
14.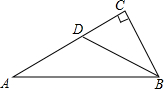 如图所示,在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,D是AC上一点,∠CBD=∠A,sin∠CDB=$\frac{2\sqrt{5}}{5}$.
如图所示,在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,D是AC上一点,∠CBD=∠A,sin∠CDB=$\frac{2\sqrt{5}}{5}$.
分析 根据在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,D是AC上一点,∠CBD=∠A,可以求得∠ABC的正弦值,∠ABC与∠CDB的关系,从而可以解答本题.
解答 解:∵在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,
∴设BC=x,则AC=2x,
∴$AB=\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{x}^{2}+(2x)^{2}}=\sqrt{5}x$,
∴sin∠ABC=$\frac{AC}{AB}=\frac{2x}{\sqrt{5}x}=\frac{2\sqrt{5}}{5}$,
∵在△ABC中,∠C=90°,D是AC上一点,∠CBD=∠A,
∴∠CDB=∠ABC,
∴sin∠CDB=$\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 本题考查解直角三角形,解题的关键明确等角的锐角三角函数值相等.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
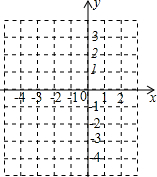 已知二次函数的图象经过(0,-3),且顶点坐标为(-1,-4).
已知二次函数的图象经过(0,-3),且顶点坐标为(-1,-4).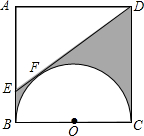 如图,以正方形ABCD边BC为直径作半圆O,过点D作直线与半圆相切于点F,交AB于点E,若AB=2cm.求:
如图,以正方形ABCD边BC为直径作半圆O,过点D作直线与半圆相切于点F,交AB于点E,若AB=2cm.求: 矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4cm,则AB=2cm,矩形ABCD的面积=4$\sqrt{3}$cm2.
矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4cm,则AB=2cm,矩形ABCD的面积=4$\sqrt{3}$cm2.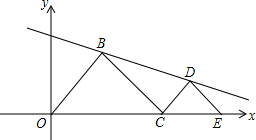 如图,E为(8,0),C是线段OE上一动点(不包括两个端点),分别以OC、CE为斜边,在第一象限作等腰Rt△OBC和等腰Rt△CDE,其中∠OBC=∠CDE=90°.设OC=a
如图,E为(8,0),C是线段OE上一动点(不包括两个端点),分别以OC、CE为斜边,在第一象限作等腰Rt△OBC和等腰Rt△CDE,其中∠OBC=∠CDE=90°.设OC=a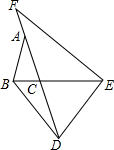 如图,△ABC中,AB=AC,点D在AC的延长线上,点E在BC的延长线上,DB=DE,∠FAB+∠F=180°,求证:EF=AD.
如图,△ABC中,AB=AC,点D在AC的延长线上,点E在BC的延长线上,DB=DE,∠FAB+∠F=180°,求证:EF=AD.