题目内容
13.在平面直角坐标系中,已知A(1,-3),B(4,-1),P(a,0),N(a+2,0).请用作图的方式在x轴上确定P、N的位置,使得四边形PABN的周长最小(保留作图痕迹,不写作法)分析 如图,作点B关于x轴的对称点B′,则B′的坐标为(4,1),把B′向左平移2个单位得到点A'(2,1),连接AA′,与x轴交于点P,把P向右平移2个单位得到N,于是得到PN=A′B′=2,推出四边形A′B′PN为平行四边形,根据平行四边形的性质得到PB′=A′N,PB=PB′,得到PB=NA′,于是推出PB+AN=AA′,此时PB+AN最小,而PN与AB的长一定,此时四边形ABDC的周长最短.
解答 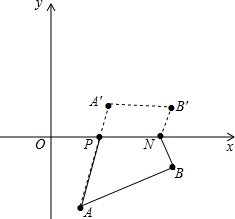 解:如图,作点B关于x轴的对称点B′,则B′的坐标为(4,1),把B′向左平移2个单位得到点A'(4,2),连接AA′,与x轴交于点N,把N向右平移2个单位得到P,′
解:如图,作点B关于x轴的对称点B′,则B′的坐标为(4,1),把B′向左平移2个单位得到点A'(4,2),连接AA′,与x轴交于点N,把N向右平移2个单位得到P,′
则四边形PABN的周长最小.
点评 本题考查了轴对称-最短路线问题:通过对称,把两条线段的和转化为一条线段,利用两点之间线段最短解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
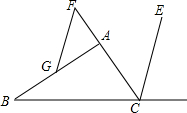 如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,求∠BAC的度数.
如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,求∠BAC的度数.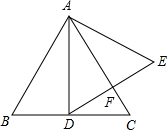 如图,在正△ABC中,AD⊥BC于点D,以AD为一边向右作正△ADE.请判断AC,DE的位置关系,并给出证明.
如图,在正△ABC中,AD⊥BC于点D,以AD为一边向右作正△ADE.请判断AC,DE的位置关系,并给出证明.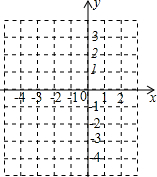 已知二次函数的图象经过(0,-3),且顶点坐标为(-1,-4).
已知二次函数的图象经过(0,-3),且顶点坐标为(-1,-4).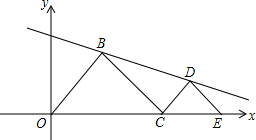 如图,E为(8,0),C是线段OE上一动点(不包括两个端点),分别以OC、CE为斜边,在第一象限作等腰Rt△OBC和等腰Rt△CDE,其中∠OBC=∠CDE=90°.设OC=a
如图,E为(8,0),C是线段OE上一动点(不包括两个端点),分别以OC、CE为斜边,在第一象限作等腰Rt△OBC和等腰Rt△CDE,其中∠OBC=∠CDE=90°.设OC=a