题目内容
16. 如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F.
如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F.(1)求证:AE=CE;
(2)求证:△AEF≌△CEB.
分析 (1)求出∠ACE=45°,证明∠EAC=∠ACE,即可解答;
(2)利用同角的余角相等,证明∠BAD=∠BCE,利用ASA证明即可解答.
解答 解:(1)∵CE⊥AB,
∴∠AEC=90°,
∵∠BAC=45°,
∴∠ACE=90°-45°=45°,
∴∠EAC=∠ACE,
∴AE=CE.
(2)∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∵∠B+∠BCE=90°,
∴∠BAD=∠BCE,
在△AEF和△CEB中,
$\left\{\begin{array}{l}{∠AEF=∠CEB}\\{AE=CE}\\{∠EAF=∠BCE}\end{array}\right.$
∴△AEF≌△CEB.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是熟记全等三角形的判定方法.

练习册系列答案
相关题目
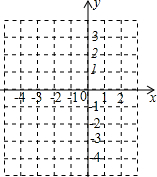 已知二次函数的图象经过(0,-3),且顶点坐标为(-1,-4).
已知二次函数的图象经过(0,-3),且顶点坐标为(-1,-4). 矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4cm,则AB=2cm,矩形ABCD的面积=4$\sqrt{3}$cm2.
矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4cm,则AB=2cm,矩形ABCD的面积=4$\sqrt{3}$cm2.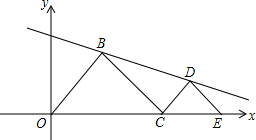 如图,E为(8,0),C是线段OE上一动点(不包括两个端点),分别以OC、CE为斜边,在第一象限作等腰Rt△OBC和等腰Rt△CDE,其中∠OBC=∠CDE=90°.设OC=a
如图,E为(8,0),C是线段OE上一动点(不包括两个端点),分别以OC、CE为斜边,在第一象限作等腰Rt△OBC和等腰Rt△CDE,其中∠OBC=∠CDE=90°.设OC=a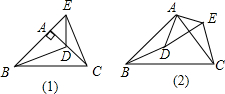
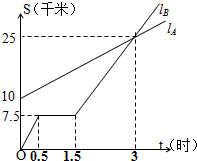 如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.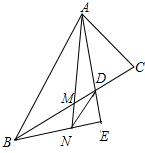 如图,已知△ABC中,M是BC的中点,AD平分∠A,B在AD上的射影为E,EB交AM于N,求证:DN∥AB.
如图,已知△ABC中,M是BC的中点,AD平分∠A,B在AD上的射影为E,EB交AM于N,求证:DN∥AB.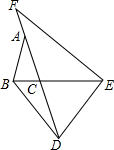 如图,△ABC中,AB=AC,点D在AC的延长线上,点E在BC的延长线上,DB=DE,∠FAB+∠F=180°,求证:EF=AD.
如图,△ABC中,AB=AC,点D在AC的延长线上,点E在BC的延长线上,DB=DE,∠FAB+∠F=180°,求证:EF=AD.