题目内容
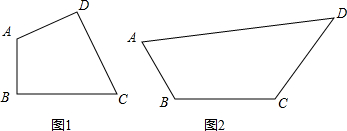
6.问题探索:(1)如图1,已知四边形ABCD中,AB=a,BC=b,∠B=∠D=90°,求:
①对角线BD长度的最大值;②四边形ABCD的最大面积;(用含有a,b的代数式表示)
(2)如图2,四边形ABCD是某市规划用地示意图,经测量得到如下数据:AB=20cm,BC=30cm,∠B=120°,∠A+∠C=195°,请你用所学到的知识探索出它的最大面积,并说明理由.(结果保留根号)
分析 (1)①由条件可知AC为直径,可知BD长度的最大值为AC的长,可求得答案;②连接AC,求得AD2+CD2,利用不等式的性质可求得AD•CD的最大值,从而可求得四边形ABCD面积的最大值;
(2)连接AC,延长CB,过点A做AE⊥CB交CB的延长线于E,可先求得△ABC的面积,结合条件可求得∠D=45°,且A、C、D三点共圆,作AC、CD中垂线,交点即为圆心O,当点D与AC的距离最大时,三角形ACD的面积最大,AC的中垂线交圆O于点D',交AC于F,FD'即为所求最大值,再求得
△ACD′的面积即可.
解答 解:(1)①因为∠B=∠D=90°,所以四边形ABCD是圆内接四边形,
AC为圆的直径,则BD长度的最大值为AC,此时BD=$\sqrt{{a^2}+{b^2}}$,
②如图1,连接AC,则AC2=AB2+BC2=a2+b2=AD2+CD2,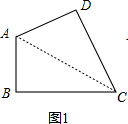
∴S△ACD=$\frac{1}{2}$AD•CD≤$\frac{1}{4}$(AD2+CD2)=$\frac{1}{4}$(a2+b2),
∴四边形ABCD的最大面积=$\frac{1}{4}$(a2+b2)+$\frac{1}{2}$ab=$\frac{1}{4}$(a2+b2+2ab);
(2)如图2,连接AC,延长CB,过点A做AE⊥CB交CB的延长线于E,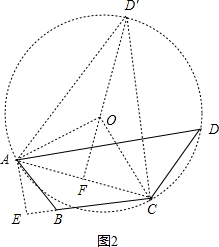
∵AB=20,∠ABE=180°-∠ABC=60°,
∴AE=AB•sin60°=10$\sqrt{3}$,EB=AB•cos60°=10,
∴S△ABC=$\frac{1}{2}$AE•BC=$\frac{1}{2}$×10$\sqrt{3}$×30=150$\sqrt{3}$,
∵BC=30,
∴EC=EB+BC=40,
∴AC=$\sqrt{A{E}^{2}+E{C}^{2}}$=10$\sqrt{19}$,
∵∠ABC=120°,∠BAD+∠BCD=195°,
∴∠D=45°,
在三角形ACD中,D角为定角,对边AC为定边,
∴A、C、D点在同一个圆上,
作AC、CD中垂线,交点即为圆心O,如图,
当点D与AC的距离最大时,三角形ACD的面积最大,AC的中垂线交圆O于点D',交AC于F,FD'即为所求最大值,
连接OA、OC,则∠AOC=2∠AD'C=90°,OA=OC,
∴△AOC,△AOF为等腰直角三角形,
∴AO=OD′=5$\sqrt{38}$,OF=AF=$\frac{1}{2}$AC=5$\sqrt{19}$,
∴D′F=OD′+OF=5$\sqrt{38}$+5$\sqrt{19}$,
∴S△ACD′=$\frac{1}{2}$AC•D′F=$\frac{1}{2}$×10$\sqrt{19}$×(5$\sqrt{38}$+5$\sqrt{19}$)=475$\sqrt{2}$+475,
∴四边形ABCD面积的最大=S△ABC+S△ACD′=150$\sqrt{3}$+475$\sqrt{2}$+475.
点评 本题为圆的综合应用,涉及知识点有圆周角定理、不等式的性质、解直角三角形及转化思想等.在(1)中注意直径是最长的弦,在(2)中确定出四边形ABCD面积最大时D点的位置是解题的关键.本题考查知识点较多,综合性很强,计算量很大,难度适中.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案| A. | y=0.05x | B. | y=3x | C. | y=60x | D. | y=0.05x+60 |
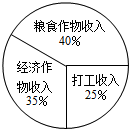 如图是某户2010年收入情况的扇形统计图,已知他2010年的总收入为6万元,则他的打工收入是( )
如图是某户2010年收入情况的扇形统计图,已知他2010年的总收入为6万元,则他的打工收入是( )| A. | 0.75万元 | B. | 1.25万元 | C. | 1.5万元 | D. | 2万元 |
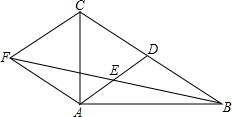 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.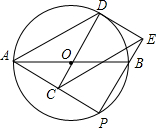 如图,AB是⊙O直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE.
如图,AB是⊙O直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE.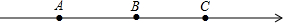 数轴上有A、B、C三个点,B点表示的数是1,C点表示的数是$\sqrt{5}$,且AB=BC,则A点表示的数是2-$\sqrt{5}$.
数轴上有A、B、C三个点,B点表示的数是1,C点表示的数是$\sqrt{5}$,且AB=BC,则A点表示的数是2-$\sqrt{5}$.