题目内容
1.已知在△ABC中,AB=AC=5,BC=6,则△ABC的外接圆的半径是$\frac{25}{8}$.分析 已知△ABC是等腰三角形,根据等腰三角形的性质,若过A作底边BC的垂线,则AD必过圆心O,在Rt△OBD中,用半径表示出OD的长,即可用勾股定理求得半径的长.
解答 解:过A作AD⊥BC于D,连接BO,
△ABC中,AB=AC,AD⊥BC,
则AD必过圆心O,
Rt△ABD中,AB=5,BD=3 ,
,
∴AD=4
设⊙O的半径为x,
Rt△OBD中,OB=x,OD=4-x,
根据勾股定理,得:OB2=OD2+BD2,
即:x2=(4-x)2+32,
解得:x=$\frac{25}{8}$,
故答案为:$\frac{25}{8}$.
点评 本题考查了三角形的外接圆、等腰三角形的性质和勾股定理等知识的综合应用,正确画出满足题意的图形并做出辅助线是解题的关键.

练习册系列答案
相关题目
9. 如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中的全等三角形共有( )
如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中的全等三角形共有( )
 如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中的全等三角形共有( )
如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中的全等三角形共有( )| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
 如图,AB=DB,BC=BE,∠1=∠2,试说明△ABE≌△DBC.
如图,AB=DB,BC=BE,∠1=∠2,试说明△ABE≌△DBC.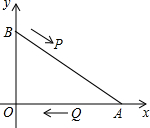 如图,在直角坐标系中,已知点A(8,0)、B(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒.解答如下问题:
如图,在直角坐标系中,已知点A(8,0)、B(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒.解答如下问题: 学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米.
学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米.