题目内容
3. 若m,n为正实数,t是关于x的方程x2+2mx=n2的一正实数根,
若m,n为正实数,t是关于x的方程x2+2mx=n2的一正实数根,①求证:(t+m)2=m2+n2
②若两条线段的长分别为m、n(如图).请画出一条长为t的线段(保留作图痕迹.不写作法).
分析 ①根据配方法解关于x的方程x2+2mx=n2得到(x+m)2═m2+n2,再根据t是关于x的方程x2+2mx=n2的一正实数根即可求解;
②利用勾股定理画出$\sqrt{{m}^{2}+{n}^{2}}$,再在长为$\sqrt{{m}^{2}+{n}^{2}}$的线段上截取长为m的线段,剩余部分就是长为t的线段.
解答 ①证明:解关于x的方程x2+2mx=n2:
x2+2mx+m2=m2+n2
(x+m)2═m2+n2,
∵t是关于x的方程x2+2mx=n2的一正实数根,
∴(t+m)2=m2+n2;
②解:作图如下:
点评 本题考查了作图-复杂作图,解一元二次方程、勾股定理等知识点,解题的关键是掌握以上知识点的内涵及其应用方法.

练习册系列答案
相关题目
13.下列命题正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 对角线相等且垂直的四边形是正方形 | |
| C. | 平行四边形的对角线互相平分 | |
| D. | 对角线相等的四边形是矩形 |
14.小明的讲义夹里放了大小相同的试卷共12页,其中语文4页,数学2页,英语6页,他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
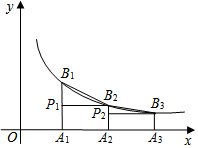 如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3═An-1An=1,分别过点A1、A2、A3、…、An作x轴的垂线,交反比例函数y=$\frac{2}{x}$(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2017=$\frac{2017}{2018}$.
如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3═An-1An=1,分别过点A1、A2、A3、…、An作x轴的垂线,交反比例函数y=$\frac{2}{x}$(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2017=$\frac{2017}{2018}$. 如图,△BCD内有一点A,∠ABC=15°,△ACD是等腰直角三角形,∠ACD=90°,BD=7,AB=3,则BC的长为4$\sqrt{2}$.
如图,△BCD内有一点A,∠ABC=15°,△ACD是等腰直角三角形,∠ACD=90°,BD=7,AB=3,则BC的长为4$\sqrt{2}$.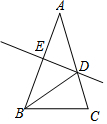 如图,△ABC中,AB的垂直平分线交AC于D,已知AC=10cm,BC=7cm,则△BCD的周长是17cm.
如图,△ABC中,AB的垂直平分线交AC于D,已知AC=10cm,BC=7cm,则△BCD的周长是17cm.