题目内容
11.如图,(n+1)个边长为2的等边三角形有一条边在同一直线上,设阴影部分△B2D1C1的面积为S1,△B3D2C2面积S2,…,△Bn+1DnCn面积Sn,则S2015值为( )
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2013\sqrt{3}}{2014}$ | D. | $\frac{2015\sqrt{3}}{2016}$ |
分析 由n+1个边长为2的等边三角形有一条边在同一直线上,则B1,B2,B3,…Bn在一条直线上,可作出直线B1B2.易求得△AB1C1的面积,然后由相似三角形的性质,易求得S1的值,同理求得S2的值,继而求得Sn的值.
解答 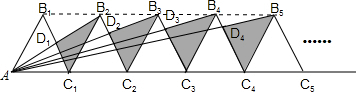 解:∵n+1个边长为2的等边三角形有一条边在同一直线上,
解:∵n+1个边长为2的等边三角形有一条边在同一直线上,
∴S△AB1C1=$\frac{1}{2}×2×\sqrt{3}$=$\sqrt{3}$,
连接B1、B2、B3、B4、B5点,显然它们共线且平行于AC1,
∵∠B1C1B2=60°,
∴AB1∥B2C1,
∴△B1C1B2是等边△,且边长=2,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=$\frac{\sqrt{3}}{2}$,
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=$\frac{2\sqrt{3}}{3}$,
同理:B3B4:AC3=1:3,
∴B3D3:D3C3=1:3,
∴S3=$\frac{3\sqrt{3}}{4}$,
则归纳可得:Sn=$\frac{n\sqrt{3}}{n+1}$,
∴S2015=$\frac{2015\sqrt{3}}{2016}$,
故选:D.
点评 此题主要考查了等边三角形的性质与三角形面积的求解方法,注意由一般到特殊的归纳方法,找到规律CnDn=$\frac{n}{n+1}$是解题的关键.

练习册系列答案
相关题目
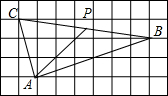 如图,正方形网格的边长为1,点A,B,C在网格的格点上,点P为BC的中点,则AP=$\frac{5\sqrt{2}}{2}$.
如图,正方形网格的边长为1,点A,B,C在网格的格点上,点P为BC的中点,则AP=$\frac{5\sqrt{2}}{2}$.
 已知:菱形ABCD的两条对角线AC、BD长分别为6、8,且AE⊥BC,垂足为E,则AE=4.8.
已知:菱形ABCD的两条对角线AC、BD长分别为6、8,且AE⊥BC,垂足为E,则AE=4.8. 在矩形ABCD中,M是AD边上的中点,N是DC边上的中点,AN与MC交于点P,若∠MCB=∠NBC+33°,则∠MPA=33°.
在矩形ABCD中,M是AD边上的中点,N是DC边上的中点,AN与MC交于点P,若∠MCB=∠NBC+33°,则∠MPA=33°.