题目内容
2.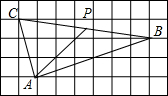 如图,正方形网格的边长为1,点A,B,C在网格的格点上,点P为BC的中点,则AP=$\frac{5\sqrt{2}}{2}$.
如图,正方形网格的边长为1,点A,B,C在网格的格点上,点P为BC的中点,则AP=$\frac{5\sqrt{2}}{2}$.
分析 首先根据网格计算出AC2=12+32=10,AB2=22+62=40,CB2=12+72=50,进而可得∠CAB=90°,然后再根据直角三角形斜边上的中线等于斜边的一半可得答案.
解答 解:AC2=12+32=10,AB2=22+62=40,CB2=12+72=50,
∵10+40=50,
∴AC2+AB2=CB2,
∴∠CAB=90°,
∵点P为BC的中点,
∴AP=$\frac{1}{2}$BC=$\frac{1}{2}$×$\sqrt{50}$=$\frac{5\sqrt{2}}{2}$.
故答案为:$\frac{5\sqrt{2}}{2}$.
点评 此题主要考查了勾股定理逆定理,以及直角三角形的性质,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
1.等边三角形的边心距、半径、边长之比为( )
| A. | 1:$\sqrt{3}$:2 | B. | 1:2:$\sqrt{3}$ | C. | 1:2$\sqrt{3}$:2 | D. | 1:2:2$\sqrt{3}$ |
7.已知关于x的二次三项式4x2-mx+25是完全平方式,则常数m的值为( )
| A. | 10 | B. | ±10 | C. | -20 | D. | ±20 |
11.如图,(n+1)个边长为2的等边三角形有一条边在同一直线上,设阴影部分△B2D1C1的面积为S1,△B3D2C2面积S2,…,△Bn+1DnCn面积Sn,则S2015值为( )


| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2013\sqrt{3}}{2014}$ | D. | $\frac{2015\sqrt{3}}{2016}$ |
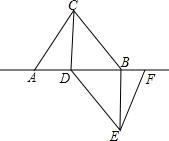 △ABC和△DEF都是边长为6cm的等边三角形,且A、D、B、F在同一直线上,连接CD、BF.
△ABC和△DEF都是边长为6cm的等边三角形,且A、D、B、F在同一直线上,连接CD、BF.