题目内容
1. 在矩形ABCD中,M是AD边上的中点,N是DC边上的中点,AN与MC交于点P,若∠MCB=∠NBC+33°,则∠MPA=33°.
在矩形ABCD中,M是AD边上的中点,N是DC边上的中点,AN与MC交于点P,若∠MCB=∠NBC+33°,则∠MPA=33°.
分析 由矩形的性质得出AD=BC,AD∥BC,∠D=∠BCN=90°,由SAS证明△ADN≌△BCN,得出∠CBN=∠DAN,求出∠MCB=∠DMC,由三角形的外角性质得出∠DMC=∠DAN+∠MPA,∠MCB=∠NBC+33°,∠CBN=∠DAN,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∠D=∠BCN=90°,
∵N为DC的中点,
∴DN=CN,
在△ADN和△BCN中,
$\left\{\begin{array}{l}{DN=CN}&{\;}\\{∠D=∠BCN}&{\;}\\{AD=BC}&{\;}\end{array}\right.$,
∴△ADN≌△BCN(SAS),
∴∠CBN=∠DAN,
∵AD∥BC,
∴∠MCB=∠DMC,
∵∠DMC=∠DAN+∠MPA,∠MCB=∠NBC+33°,∠CBN=∠DAN,
∴∠MPA=33°.
故答案为:33°.
点评 本题考查了矩形的性质、全等三角形的判定与性质、平行线的性质、三角形的外角性质;熟练掌握矩形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
11.如图,(n+1)个边长为2的等边三角形有一条边在同一直线上,设阴影部分△B2D1C1的面积为S1,△B3D2C2面积S2,…,△Bn+1DnCn面积Sn,则S2015值为( )


| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2013\sqrt{3}}{2014}$ | D. | $\frac{2015\sqrt{3}}{2016}$ |
10.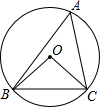 如图,⊙O是△ABC的外接圆,∠BCO=40°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BCO=40°,则∠A的度数等于( )
 如图,⊙O是△ABC的外接圆,∠BCO=40°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BCO=40°,则∠A的度数等于( )| A. | 60° | B. | 50° | C. | 45° | D. | 40° |
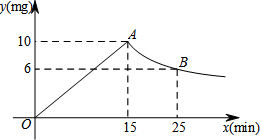 据媒体报道,近期“甲型H7N9禽流感”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“甲型H7N9禽流感”,对教室进行“熏药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示,第一段是线段OA,第二段是一个反比例函数的图象(即图中A点及其右侧的部分),根据图象所示信息,解答下列问题:
据媒体报道,近期“甲型H7N9禽流感”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“甲型H7N9禽流感”,对教室进行“熏药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示,第一段是线段OA,第二段是一个反比例函数的图象(即图中A点及其右侧的部分),根据图象所示信息,解答下列问题: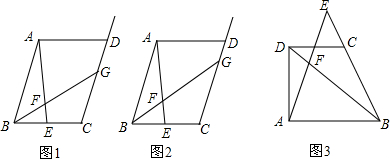
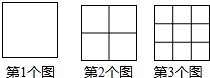 观察下面图形我们可以发现:第1个图中有1个正方形,第2个图中有5个正方形,按照这种规律变化下去…
观察下面图形我们可以发现:第1个图中有1个正方形,第2个图中有5个正方形,按照这种规律变化下去…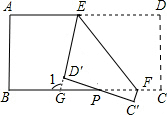 如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠BFC′=70°,则∠1=110°.
如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠BFC′=70°,则∠1=110°.