题目内容
16. 将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m,n)表示第m排的第n个数,如(4,2)表示的数是 $\sqrt{6}$,则(5,4)与(18,15)表示的两数之积是2$\sqrt{3}$.
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m,n)表示第m排的第n个数,如(4,2)表示的数是 $\sqrt{6}$,则(5,4)与(18,15)表示的两数之积是2$\sqrt{3}$.
分析 所给一系列数是4个数一循环,得出(5,4)与(18,15)是第几个数,再除以4,根据余数得到相应循环的数即可.
解答 解:∵前4排的数共有1+2+3+4=10个,
∴(5,4)表示第10+4=14个数,
∵14÷4=3余2,
∴(5,4)表示的数为$\sqrt{2}$,
同理可得,(18,15)表示的数为$\sqrt{6}$,
∴(5,4)与(18,15)表示的两数之积是$\sqrt{12}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 此题主要考查了数字的变化规律与二次根式的运算,对于找规律的题目找准变化规律是关键.

练习册系列答案
相关题目
5.若非零实数a、b满足4a2+b2=4ab,则$\frac{b}{a}$=( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
 如图,⊙O是△ABC的外接圆,CG是直径,CE⊥AB于E,CA=8,CB=12,CE=6,求CG的长.
如图,⊙O是△ABC的外接圆,CG是直径,CE⊥AB于E,CA=8,CB=12,CE=6,求CG的长. )×(-9)÷(-
)×(-9)÷(- )
) 如图,已知∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.当AB⊥OM,且△ADB有两个相等的角时,∠OAC的度数为10°、25°、40°.
如图,已知∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.当AB⊥OM,且△ADB有两个相等的角时,∠OAC的度数为10°、25°、40°.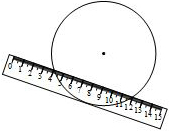 如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为10cm的圆相切时,另一边与圆两个交点处的读数恰好为“4”和“12”(单位:cm),则刻度尺的宽为2cm.
如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为10cm的圆相切时,另一边与圆两个交点处的读数恰好为“4”和“12”(单位:cm),则刻度尺的宽为2cm. 如图,⊙O是四边形ABCD的内切圆,切点为E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四边形ABCD的周长.
如图,⊙O是四边形ABCD的内切圆,切点为E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四边形ABCD的周长.