题目内容
15.函数y=2x+4的图象与x轴,y轴的交点为A,B,若AB=2$\sqrt{5}$.则原点O到AB的距离是( )| A. | $\sqrt{5}$ | B. | $\frac{4\sqrt{5}}{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{2\sqrt{5}}{3}$ |
分析 根据题意得出图象与x轴,y轴交点坐标,进而利用三角形面积求法得出答案.
解答  解:如图所示:过点O作OD⊥AB于点D,
解:如图所示:过点O作OD⊥AB于点D,
∵函数y=2x+4的图象与x轴,y轴的交点为A,B,
∴y=0时,0=2x+4,
解得:x=-2,
当x=0时,y=4,
故AO=2,BO=4,
∴AO×BO=DO×AB,
则2×4=2$\sqrt{5}$•DO,
解得:DO=$\frac{4\sqrt{5}}{5}$.
故选:B.
点评 此题主要考查了一次函数图象上点的坐标特征,正确得出图象与x轴,y轴交点坐标是解题关键.

练习册系列答案
相关题目
4.在分式$\frac{a}{b+c}$中,a,b,c都缩小到原来的一半,则分式的值是原来的( )
| A. | 1倍 | B. | 一半 | C. | 2倍 | D. | 4倍 |
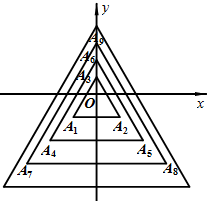 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A22的坐标是(-8,-8).
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A22的坐标是(-8,-8).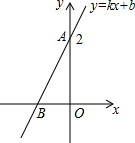 如图所示,直线AB是一次函数y=kx+b的图象.若AB=$\sqrt{5}$,则函数解析式为y=2x+2.
如图所示,直线AB是一次函数y=kx+b的图象.若AB=$\sqrt{5}$,则函数解析式为y=2x+2.