Question

17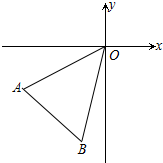．如图，平面直角坐标系中，A（-3，-2）、B（-1，-4）
（1）直接写出：S_△OAB=5；
（2）延长AB交y轴于P点，求P点坐标；
（3）Q点在y轴上，以A、B、O、Q为顶点的四边形面积为6，求Q点坐标．

Answer 1

分析 （1）延长AB交y轴于P点，如图，利用待定系数法求出直线AB的解析式为y=-x-5，则得到P（0，-5），然后根据三角形面积公式和利用S_△OAB=S_△AOP-S_△OBP进行计算即可；
（2）由（1）得到P点的坐标；
（3）分类讨论：当Q在y轴的正半轴上时，利用S_{四边形ABOQ}=S_△AOB+S_△AOQ得到S_△AOQ=1，再根据三角形面积公式求出OQ．从而得到Q点坐标；当Q在y轴的负半轴上时，利用S_{四边形ABOQ}=S_△AOB+S_△BOQ得到S_△BOQ=1，再根据三角形面积公式求出OQ．从而得到Q点坐标．

解答 解：（1）延长AB交y轴于P点，如图，
设直线AB的解析式为y=kx+b，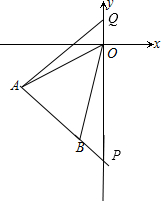
把A（-3，-2）、B（-1，-4）代入得$\left\{\begin{array}{l}{-3k+b=-2}\\{-k+b=-4}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=-1}\\{b=-5}\end{array}\right.$．
所以直线AB的解析式为y=-x-5，
当x=0时，y=-x-5=-5，则P（0，-5），
所以S_△OAB=S_△AOP-S_△OBP
=$\frac{1}{2}$×5×3-$\frac{1}{2}$×5×1
=5．
故答案为5；
（2）由（1）得到P点的坐标为（0，-5）；
（3）当Q在y轴的正半轴上时，∵S_{四边形ABOQ}=S_△AOB+S_△AOQ，
∴S_△AOQ=6-5=1，
∴$\frac{1}{2}$×3×OQ=1，
解得OQ=$\frac{2}{3}$．
则此时Q点的坐标为（0，$\frac{2}{3}$）；
当Q在y轴的负半轴上时，
∵S_{四边形ABOQ}=S_△AOB+S_△BOQ，
∴S_△BOQ=1，
∴S_△AOQ=6-5=1，
∴$\frac{1}{2}$×1×OQ=1，
解得OQ=2，
则此时Q点的坐标为（0，-2），
即Q点坐标为（0，$\frac{2}{3}$）或（0，-2）．

点评 本题考查了坐标与图形性质：利用点的坐标求相应线段的长和判断线段与坐标轴的位置关系．也考查了三角形面积公式．第（3）问要分类讨论．