题目内容
6.反比例函数y=$\frac{{m}^{2}}{x}$图象经过点(1,4),且双曲线y=$\frac{m}{x}$位于二、四象限,则m=-2.分析 首先根据待定系数法确定m的值,然后根据其图象位置确定所处的象限,从而确定m的值.
解答 解:∵反比例函数y=$\frac{{m}^{2}}{x}$图象经过点(1,4),
∴m2=1×4=4,
∴m=±2,
∵双曲线y=$\frac{m}{x}$位于二、四象限,
∴m<0,
∴m=-2,
故答案为:-2.
点评 考查了反比例函数的性质,解答此题的关键是要熟知反比例函数图象的性质及用待定系数法求反比例函数的解析式.
反比例函数图象的性质:
(1)当k>0时,反比例函数的图象位于一、三象限;
(2)当k<0时,反比例函数的图象位于二、四象限.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
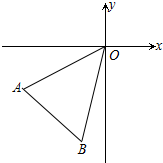 如图,平面直角坐标系中,A(-3,-2)、B(-1,-4)
如图,平面直角坐标系中,A(-3,-2)、B(-1,-4)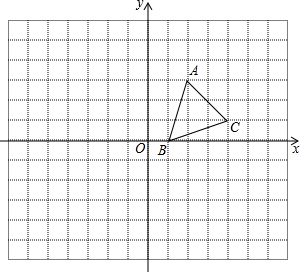 如图,方格纸中的每个小方格都是边长为1单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
如图,方格纸中的每个小方格都是边长为1单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0) =-10,
=-10, =4,
=4, =1,求:
=1,求: 的值.
的值.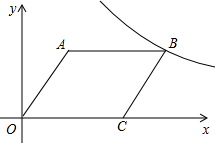 如图所示,在平面直角坐标系中,已知四边形AOBC都是菱形,且A(3,4),若在第一象限,反比例函数y=$\frac{k}{x}$的图象经过点B,写出点B和点C的坐标,求反比例函数解析式.
如图所示,在平面直角坐标系中,已知四边形AOBC都是菱形,且A(3,4),若在第一象限,反比例函数y=$\frac{k}{x}$的图象经过点B,写出点B和点C的坐标,求反比例函数解析式.
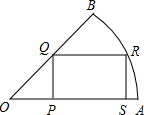 如图,扇形中∠AOB=45°,半径OB=2,矩形PQRS的顶点P、S在半径OA上,Q在半径OB上,R在弧AB上,连接OR.
如图,扇形中∠AOB=45°,半径OB=2,矩形PQRS的顶点P、S在半径OA上,Q在半径OB上,R在弧AB上,连接OR.