题目内容
17.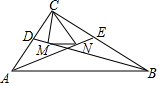 在Rt△ABC中,∠ACB=90°,AE,BD是角平分线,CM⊥BD于M,CN⊥AE于N,若AC=6,BC=8,则MN=2.
在Rt△ABC中,∠ACB=90°,AE,BD是角平分线,CM⊥BD于M,CN⊥AE于N,若AC=6,BC=8,则MN=2.
分析 延长CM交AB于G,延长CN交AB于H,证明△BMC≌△BMG,得到BG=BC=8,CM=MG,同理得到AH=AC=6,CN=NH,根据三角形中位线定理计算即可.
解答 解:延长CM交AB于G,延长CN交AB于H,
∵∠ACB=90°,AC=6,BC=8,
∴AB=10,
在△BMC和△BMG中,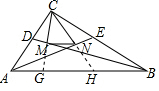
$\left\{\begin{array}{l}{∠MBC=∠MBG}\\{BM=MB}\\{∠BMC=∠BMG}\end{array}\right.$,
∴△BMC≌△BMG,
∴BG=BC=8,CM=MG,
∴AG=2,
同理,AH=AC=6,CN=NH,
∴GH=4,
∴MN=$\frac{1}{2}$GH=2,
故答案为:2.
点评 本题考查的是三角形中位线定理、全等三角形的判定和性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
7.用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的底面周长是( )
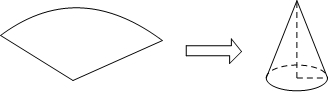

| A. | 2π cm | B. | 3π cm | C. | 4π cm | D. | 5π cm |
12.已知x=-1,y=2是二元一次方程组3x+2y=m,nx-y=1的解,则m-n的值是( )
| A. | 0 | B. | -2 | C. | 1 | D. | 4 |
2.下列计算正确的是( )
| A. | 3m+2y=5my | B. | 3a2+2a3=5a5 | C. | 4a2-3a2=1 | D. | -2ba2+a2b=-a2b |
 某长方体包装盒的表面积为146cm2,其展开图如图所示.求这个包装盒的体积.
某长方体包装盒的表面积为146cm2,其展开图如图所示.求这个包装盒的体积.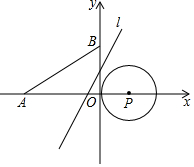 如图,平面直角坐标系中,点P的坐标为(1,0),⊙P的半径为1,点A的坐标为(-3,0),点B在y轴的正半轴上,且OB=$\sqrt{3}$.若直线1:y=$\sqrt{3}$x+m从点B开始沿y轴向下平移,线段AB与线段A′B′关于直线1对称.若线段A′B′与⊙P只有一个公共点,则m的值为$\sqrt{3}$或-$\frac{\sqrt{3}}{3}$.
如图,平面直角坐标系中,点P的坐标为(1,0),⊙P的半径为1,点A的坐标为(-3,0),点B在y轴的正半轴上,且OB=$\sqrt{3}$.若直线1:y=$\sqrt{3}$x+m从点B开始沿y轴向下平移,线段AB与线段A′B′关于直线1对称.若线段A′B′与⊙P只有一个公共点,则m的值为$\sqrt{3}$或-$\frac{\sqrt{3}}{3}$.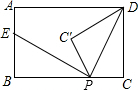 如图,在矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落在点C’处,作么BPC'的角平分线交AB于点E.设BP=x,BE=y,给出如下结论:
如图,在矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落在点C’处,作么BPC'的角平分线交AB于点E.设BP=x,BE=y,给出如下结论: