题目内容
在平面直角坐标系中,有点A(m,0),B(0,n),且m,n满足n=
.
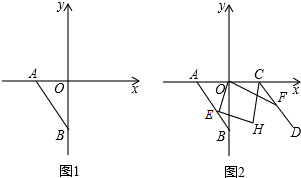
(1)求A、B两点坐标;
(2)如图1,若P(1,a),且△PAB的面积为6,求a的值;
(3)如图2,若点C为x轴正半轴上一点,过C作CD∥AB,E为线段AB上一点,过O作OF⊥OE交CD于F,其中∠BEH=
∠BEO,∠FCH=
∠FCO.试写出∠H与∠BOF之间的数量关系,并证明你的结论.
| ||||
| m-2 |

(1)求A、B两点坐标;
(2)如图1,若P(1,a),且△PAB的面积为6,求a的值;
(3)如图2,若点C为x轴正半轴上一点,过C作CD∥AB,E为线段AB上一点,过O作OF⊥OE交CD于F,其中∠BEH=
| 1 |
| 3 |
| 1 |
| 3 |
考点:坐标与图形性质,三角形的面积,三角形内角和定理
专题:
分析:(1)运用二次根式及分母有意义的条件求解.
(2)根据P点的不同位置讨论①当点P在x轴上方时,②当点P在x轴时,③当点P在x轴下方时,运用△PAB的面积为6,求出a的值.
(3)由直角关系得出∠BOF=∠AOE,由三角形外角得出∠BEO=∠BAO+∠AOE,∠1=180°-∠FCO,再由CD∥AB,得出∠BAO=∠1,即可得出∠BEO+∠FCO=180°+∠BOF,过点H作AB的平行线,可得∠H=
(∠BEO+∠FCO).从而得出结论.
(2)根据P点的不同位置讨论①当点P在x轴上方时,②当点P在x轴时,③当点P在x轴下方时,运用△PAB的面积为6,求出a的值.
(3)由直角关系得出∠BOF=∠AOE,由三角形外角得出∠BEO=∠BAO+∠AOE,∠1=180°-∠FCO,再由CD∥AB,得出∠BAO=∠1,即可得出∠BEO+∠FCO=180°+∠BOF,过点H作AB的平行线,可得∠H=
| 1 |
| 3 |
解答:解:(1)由n=
得
,
解得m=-2,
∴n=
=-3,
∴A(-2,0),B(0,-3);
(2)①当点P在x轴上方时,如图1,BP与x轴交于点M,
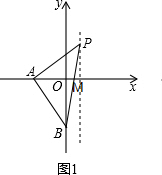
设BP所在的直线为y=k1x+b1,
把B(0,-3),P(1,a)代入,
得
,解得
,
y=(3+a)x-3,
∴M(
,0),
∴AM=2+
,
∵△PAB的面积=△AMP的面积+△AMB的面积,
∴
×(2+
)×a+
×(2+
)×3=6,
解得a=
;
②当点P在x轴上时,如图2,
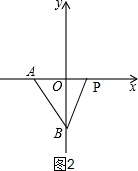
△PAB的面积=
×AP×OB=
≠6故不成立;
③当点P在x轴下方时,如图3,BP与y轴交于点M,
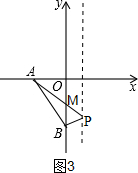
设BP所在的直线为y=k2x+b2,
把A(-2,0),P(1,a)代入y=k2x+b2,
得
,解得
,
求得AP所在的直线解析式为:y=
x+
,
∴M(0,
);
∴BM=|
+3|,
∵△PAB的面积=△ABM的面积+△PMB的面积,
×|
+3|×2+
×|
+3|×1=6,
解得,a=-
,a=
不合题意,
综上所述a的值为:
或-
;
(3)3∠H-∠BOF=180°.理由如下:
如下图4,

∵OF⊥OE,
∴∠EOF=90°,
∵∠BOF+∠BOE=∠AOE+∠BOE=90°,
∴∠BOF=∠AOE,
∵∠BEO=∠BAO+∠AOE,∠1=180°-∠FCO,
又∵CD∥AB,
∴∠BAO=∠1,
∴∠BEO=180°-∠FCO+∠AOE,
∴∠BEO+∠FCO=180°+∠BOF.
过点H作AB的平行线,可得∠H=∠BEH+∠FCH=
∠BEO+
∠FCO=
(∠BEO+∠FCO),
∴∠BEO+∠FCO=3∠H,
∴3∠H=180°+∠BOF即3∠H-∠BOF=180°,
| ||||
| m-2 |
|
解得m=-2,
∴n=
| 12 |
| -4 |
∴A(-2,0),B(0,-3);
(2)①当点P在x轴上方时,如图1,BP与x轴交于点M,

设BP所在的直线为y=k1x+b1,
把B(0,-3),P(1,a)代入,
得
|
|
y=(3+a)x-3,
∴M(
| 3 |
| 3+a |
∴AM=2+
| 3 |
| 3+a |
∵△PAB的面积=△AMP的面积+△AMB的面积,
∴
| 1 |
| 2 |
| 3 |
| 3+a |
| 1 |
| 2 |
| 3 |
| 3+a |
解得a=
| 3 |
| 2 |
②当点P在x轴上时,如图2,

△PAB的面积=
| 1 |
| 2 |
| 9 |
| 2 |
③当点P在x轴下方时,如图3,BP与y轴交于点M,

设BP所在的直线为y=k2x+b2,
把A(-2,0),P(1,a)代入y=k2x+b2,
得
|
|
求得AP所在的直线解析式为:y=
| a |
| 3 |
| 2a |
| 3 |
∴M(0,
| 2a |
| 3 |
∴BM=|
| 2a |
| 3 |
∵△PAB的面积=△ABM的面积+△PMB的面积,
| 1 |
| 2 |
| 2a |
| 3 |
| 1 |
| 2 |
| 2a |
| 3 |
解得,a=-
| 21 |
| 2 |
| 3 |
| 2 |
综上所述a的值为:
| 3 |
| 2 |
| 21 |
| 2 |
(3)3∠H-∠BOF=180°.理由如下:
如下图4,

∵OF⊥OE,
∴∠EOF=90°,
∵∠BOF+∠BOE=∠AOE+∠BOE=90°,
∴∠BOF=∠AOE,
∵∠BEO=∠BAO+∠AOE,∠1=180°-∠FCO,
又∵CD∥AB,
∴∠BAO=∠1,
∴∠BEO=180°-∠FCO+∠AOE,
∴∠BEO+∠FCO=180°+∠BOF.
过点H作AB的平行线,可得∠H=∠BEH+∠FCH=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴∠BEO+∠FCO=3∠H,
∴3∠H=180°+∠BOF即3∠H-∠BOF=180°,
点评:本题主要考查了坐标与图形的性质,三角形的面积及三角形内角和定理,解题的关键是能根据P点的不同位置进行讨伦求值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中,是假命题的是( )
| A、两条直线都与第三条直线平行,则这两条直线也互相平行 | ||||
| B、垂线段最短 | ||||
C、如果a>b>0,那么
| ||||
| D、同位角相等 |
已知a,b为非零有理数,下面四个不等式组中,解集有可能为-2<x<2的不等式组是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 (1)先化简,再求值:(a-2)(a+2)+3(a+2)2-6a(a+2),其中a=2.
(1)先化简,再求值:(a-2)(a+2)+3(a+2)2-6a(a+2),其中a=2.