题目内容
1.用公式法解下列方程:(1)x2-2x-8=0;
(2)4x2+8x+1=0;
(3)3y2+1=2$\sqrt{3}$y;
(4)x2+4x+10=1-8x.
分析 要运用公式法解一元二次方程,首先要保证方程是一般形式,若不是一般形式要转化为一般形式,然后找出a,b,c,算出b2-4ac,若b2-4ac≥0,把a,b,c代入求根公式,就可求出方程的解,若b2-4ac<0,则方程无实数根.
解答 解:(1)a=1,b=-2,c=-8,
b2-4ac=(-2)2-4×1×(-8)=36>0,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{2±\sqrt{36}}{2}$=$\frac{2±6}{2}$,
∴x1=4,x2=-2;
(2)a=4,b=8,c=1,
b2-4ac=82-4×4×1=48>0,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-8±\sqrt{48}}{8}$=$\frac{-8±4\sqrt{3}}{8}$
∴x1=$\frac{-2+\sqrt{3}}{2}$,x2=$\frac{-2-\sqrt{3}}{2}$;
(3)原方程可化为3y2-2$\sqrt{3}$y+1=0.
a=3,b=-2$\sqrt{3}$,c=1,
b2-4ac=(-2$\sqrt{3}$)2-4×3×1=0,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{2\sqrt{3}±\sqrt{0}}{6}$
∴x1=x2=$\frac{\sqrt{3}}{3}$;
(4)原方程可化为x2+12x+9=0.
a=1,b=12,c=9,
b2-4ac=122-4×1×9=108>0,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-12±\sqrt{108}}{2}$=$\frac{-12±6\sqrt{3}}{2}$,
∴x1=-6+3$\sqrt{3}$,x2=-6-3$\sqrt{3}$.
点评 本题着重考查的是用公式法解一元二次方程,需要注意的是:要用公式法解一元二次方程,首先要保证一元二次方程是一般形式ax2+bx+c=0(a≠0).

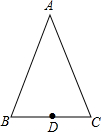 如图,等腰三角形ABC的底边BC的长为6cm,面积是27cm2,D为BC边长的中点.
如图,等腰三角形ABC的底边BC的长为6cm,面积是27cm2,D为BC边长的中点.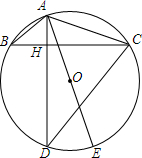 如图,已知AE为⊙O的直径,△ABC内接于⊙O,AD⊥BC于H交⊙O于D.
如图,已知AE为⊙O的直径,△ABC内接于⊙O,AD⊥BC于H交⊙O于D.