题目内容
11．已知线段m=10mm，n=2cm，e=$\sqrt{2}$cm．d=2$\sqrt{2}$cm，试判断m，n，e，d是否是成比例线段．分析 先分别计算出$\frac{m}{n}$=$\frac{1}{2}$，$\frac{e}{d}$=$\frac{\sqrt{2}}{2\sqrt{2}}$=$\frac{1}{2}$，则$\frac{m}{n}$=$\frac{e}{d}$，根据根据成比例线段的定义进行判断．
解答 解：∵m=1cm，n=2cm，e=$\sqrt{2}$cm．d=2$\sqrt{2}$cm，
∴$\frac{m}{n}$=$\frac{1}{2}$，$\frac{e}{d}$=$\frac{\sqrt{2}}{2\sqrt{2}}$=$\frac{1}{2}$，
∴$\frac{m}{n}$=$\frac{e}{d}$，
∴m，n，e，d成比例线段．
点评 本题考查了比例线段：对于四条线段a、b、c、d，如果其中两条线段的比（即它们的长度比）与另两条线段的比相等，如 a：b=c：d（即ad=bc），我们就说这四条线段是成比例线段，简称比例线段．本题的关键是单位统一．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
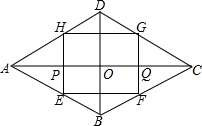如图，在菱形ABCD中，两条对角线长是AC=10，BD=6，F是线段AO上一点（不与A、O重合），Q是线段OC上一点，且AP=CQ，分别将∠BAD和∠BCD折叠，使A、C两点都在对角线AC上，折痕分别是EH和FG，EH过P点，FG过Q点，连接EF、HG，再把折叠部分铺平．