题目内容
10．若（|m|-1）x2-（m+1）x+7=0是一元一次方程，则m的值是1．分析 根据一元一次方程的定义得到|m|-1=0且-（m+1）≠0，先解绝对值方程得到m=≠1，然后利用m+1≠0可确定m的值为1．
解答 解：根据题意得|m|-1=0且-（m+1）≠0，
解得m=1．
故答案为1．
点评 本题考查了一元一次方程的定义：只含有一个未知数（元），且未知数的次数是1，这样的方程叫一元一次方程．通常形式是ax+b=0（a，b为常数，且a≠0）．
练习册系列答案
学习实践园地系列答案
相关题目
15．如果分式$\frac{1}{{x}^{2}+x-1}$有意义，则（ ）
| A． | x≠1-$\sqrt{5}$ | B． | x≠$\frac{1-\sqrt{5}}{2}$ | C． | x≠-1±$\sqrt{5}$ | D． | x≠$\frac{-1±\sqrt{5}}{2}$ |
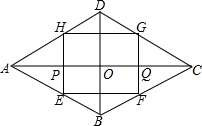如图，在菱形ABCD中，两条对角线长是AC=10，BD=6，F是线段AO上一点（不与A、O重合），Q是线段OC上一点，且AP=CQ，分别将∠BAD和∠BCD折叠，使A、C两点都在对角线AC上，折痕分别是EH和FG，EH过P点，FG过Q点，连接EF、HG，再把折叠部分铺平．