��Ŀ����
12����ƽ��ֱ������ϵ�У������֮�����һ�ֱ任T���ڱ任T�������£���P��x��y������Ϊ��P�䣨2x-y��3x-2y+3�������磺��P������Ϊ��1��0��ʱ���ڱ任T�������±�Ϊ��P�䣨2��1-0��3��1-2��0+3������ΪP�䣨2��6������1������M�ڱ任T�������±�ΪM�䣨1��-1�������M�����ꣻ
��2������N��$\frac{m}{4}$��m���ڱ任T�������±�Ϊ�Ķ�Ӧ��N���ڵڶ����ޣ���ʵ��m��ȡֵ��Χ��
��3����ƽ��ֱ������ϵ�ϵ�����һ��Q��x��y���ڱ任T�������¶�Ӧ��ΪQ�䣬���Ƿ����һ�κ���y=kx+b��ʹ�õ�Q��Q�䶼�����һ�κ�����ͼ���ϣ������ڣ����k��b��ֵ���������ڣ���˵�����ɣ�
���� ��1���������M�������ǣ�x��y�������ڱ任T�������£���M��x��y������Ϊ��M�䣨2x-y��3x-2y+3����Ȼ����ݵ�M��������ǣ�1��-1�����г���Ԫһ�η����飬���x��y��ֵ�����������M�����꣮
��2�����������N��$\frac{m}{4}$��m���ڱ任T�������µĵ�N��������Ƕ��٣�Ȼ����ݵ�N���ڵڶ����ޣ��ɵõ�N��ĺ�����С��0�����������0�����ʵ��m��ȡֵ��Χ���ɣ�
��3���ٵ�x=yʱ��������һ�κ���y=kx+b��ʹ�õ�Q��Q�䶼�����һ�κ�����ͼ���ϣ��ڵ�x��yʱ������һ�κ���y=kx+b��ʹ�õ�Q��Q�䶼�����һ�κ�����ͼ���ϣ����ݵ�Q��Q�䶼��һ�κ���y=kx+b��ͼ���ϣ��г���Ԫһ�η����飬���k��b��ֵ���Ƕ��ټ��ɣ�
��� �⣺��1�����M�������ǣ�x��y����
���ڱ任T�������£���M��x��y������Ϊ��M�䣨2x-y��3x-2y+3����
��$\left\{\begin{array}{l}{2x-y=1}\\{3x-2y+3=-1}\end{array}\right.$
���$\left\{\begin{array}{l}{x=6}\\{y=11}\end{array}\right.$
���M�������ǣ�6��11����
��2��2x-y=2��$\frac{m}{4}$-m=$\frac{m}{2}-m=-\frac{m}{2}$
3x-2y+3=3��$\frac{m}{4}$-2m+3=$\frac{3}{4}m$-2m+3=-$\frac{5}{4}m+3$
�ߵ�N���ڵڶ����ޣ�
��$\left\{\begin{array}{l}{-\frac{m}{2}��0}\\{-\frac{5}{4}m+3��0}\end{array}\right.$
���0��m��2.4��
��ʵ��m��ȡֵ��Χ��0��m��2.4��
��3���ٵ�x=yʱ��������һ�κ���y=kx+b��ʹ�õ�Q��Q�䶼�����һ�κ�����ͼ���ϣ�
�ڵ�x��yʱ������һ�κ���y=kx+b��ʹ�õ�Q��Q�䶼�����һ�κ�����ͼ���ϣ�
�ٵ�x=yʱ��
�ߵ�Q��x��x���ڱ任T�������¶�Ӧ��ΪQ�䣨x��x+3����
�����һ�κ���y=kx+b��ʹ�õ�Q��Q�䶼�����һ�κ�����ͼ���ϣ�
�ڵ�x��yʱ����Q��x��y���ڱ任T�������¶�Ӧ��ΪQ�䣨2x-y��3x-2y+3����
�ߵ�Q��Q�䶼��һ�κ���y=kx+b��ͼ���ϣ�
��$\left\{\begin{array}{l}{y=kx+b}\\{3x-2y+3=k��2x-y��+b}\end{array}\right.$
���$\left\{\begin{array}{l}{k=3-\frac{3}{y-x}}\\{b=y-3x+\frac{3x}{y-x}}\end{array}\right.$
�൱x��yʱ������һ�κ���y=kx+b��ʹ�õ�Q��Q�䶼�����һ�κ�����ͼ���ϣ���ʱk=3-$\frac{3}{y-x}$��b=y-3x+$\frac{3x}{y-x}$��
���� ��1��������Ҫ������һ�κ����ۺ��⣬�����˷������������������˷�������˼���Ӧ�ã������˴���֪����ͼ���л�ȡ��Ϣ���������û�ȡ����Ϣ�����Ӧ�������������
��2����������˸������ĵ���������Լ����α任��֪ʶ��Ҫ�������գ�

| A�� | 7 | B�� | 8 | C�� | 9 | D�� | 18 |
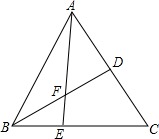 ��ͼ���ڡ�ABC�У�E��BC���ϵ�һ�㣬EC=2BE����D��AB���е㣬��S��ABC=18����S�ı���CDFE�������
��ͼ���ڡ�ABC�У�E��BC���ϵ�һ�㣬EC=2BE����D��AB���е㣬��S��ABC=18����S�ı���CDFE�������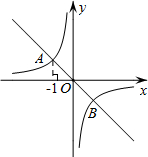 ��֪����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=-x��ͼ���뷴��������y=-$\frac{1}{x}$��ͼ����A��B���㣮
��֪����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=-x��ͼ���뷴��������y=-$\frac{1}{x}$��ͼ����A��B���㣮