题目内容
11.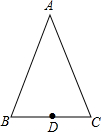 如图,等腰三角形ABC的底边BC的长为6cm,面积是27cm2,D为BC边长的中点.
如图,等腰三角形ABC的底边BC的长为6cm,面积是27cm2,D为BC边长的中点.(1)作腰AB的垂直平分线EF交AB于E,交AC于F(尺规作图,保留痕迹.不写作法):
(2)P为(1)中线段EF上的一个动点,求△PBD的最短周长.
分析 (1)利用作已知线段的垂直平分线的方法作图即可;
(2)连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AB的垂直平分线可知,点B关于直线EF的对称点为点A,故AD的长为BP+PD的最小值,由此即可得出△PBD的最短周长.
解答 解:(1)作图如下:
(2)如图,
连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×6×AD=27,解得AD=9cm,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BP+PD的最小值,
∴△BDP的周长最短=(BP+PD)+BD=AD+$\frac{1}{2}$BC=9+$\frac{1}{2}$×6=12cm.
点评 本题主要考查了作图-复杂作图,等腰三角形及中垂线的性质,解题的关键是正确作出图形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知代数式3x2-6x+3的值为9,则代数式x2-2x+6的值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 18 |
19.已知点M(a,2),B(3,b)关于y轴对称,则(a+b)2014的值( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
6.有一根长60cm的铁丝,用它围成一个矩形,写出矩形面积S(cm2)与它的一边长x(cm)之间的函数关系式为( )
| A. | S=60x | B. | S=x(60-x) | C. | S=x(30-x) | D. | S=30x |
 某正方体盒子,如图左边下方A处有一只蚂蚁,从A处爬行到侧棱GF上的中点M点处,如果蚂蚁爬行路线最短,请画出这条最短路线图.
某正方体盒子,如图左边下方A处有一只蚂蚁,从A处爬行到侧棱GF上的中点M点处,如果蚂蚁爬行路线最短,请画出这条最短路线图.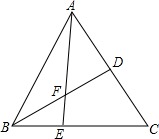 如图,在△ABC中,E是BC边上的一点,EC=2BE,点D是AB的中点,且S△ABC=18,则S四边形CDFE的面积?
如图,在△ABC中,E是BC边上的一点,EC=2BE,点D是AB的中点,且S△ABC=18,则S四边形CDFE的面积?