Question

20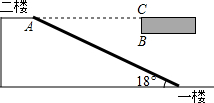．如图，某大型商场在一楼至二楼之间安装有电梯，二楼地板厚BC为0.24米，AC=7米．
（1）小明身高1.85米，他乘电梯会有碰头危险吗？
（2）该商场的上货员用推车搬运货物时，货车上货物堆放的限高是多少米？（参考数据：sin18°=0.31，cos18°=0.95，tan18°=0.32）

Answer 1

分析 （1）延长CB交电梯于点D，在Rt△ACD中，求出CD的长度，然后根据CB=0.24米，求出BD的长度，然后跟1.85米进行比较；
（2）过点B作BE⊥AD交AD于点E，在Rt△BDE中求出BE的长度即为限高．

解答 解：（1）延长CB将电梯于点D，
则△ACD为直角三角形，
∵AC=7米，∠CAD=18°，
∴CD=ACtan18°=7×0.31≈2，17（米），
∴BD=2.17-0.24=1.93＞1.85，
故小明乘电梯没有碰头危险；
（2）过点B作BE⊥AD交AD于点E，
在Rt△BDE中，
∵BD=1.93米，∠EBD=18°，
∴BE=BDcos18°≈1.83（米）．
∴货车上货物堆放的限高是1.83米．

点评 本题考查了解直角三角形的应用，解答本题的关键是根据坡度构造直角三角形，利用三角函数的知识求解直角三角形，难度适中．