题目内容
5．
△ABC中，∠C=90°，∠ABC=45°，D为AC上一点，∠DBC=30°，求AD：AB的值．
分析 根据特殊角的三角函数值关系表示出AD，DC，BC，AB的长，进而得出答案．
解答 解：∵∠C=90°，∠ABC=45°，∠DBC=30°，
∴BC=AC，BC=$\frac{DC}{tan30°}$，
设DC=x，则BC=AC=$\sqrt{3}$x，
∴AD=（$\sqrt{3}$-1）x，AB=$\sqrt{6}$x，
∴AD：BC=（$\sqrt{3}$-1）x：$\sqrt{6}$x=（$\sqrt{3}$-1）：$\sqrt{6}$．
点评 此题主要考查了解直角三角形，正确用同一未知数表示出各边长是解题关键．
练习册系列答案
相关题目
为了给学生提供更好的学习生活环境，重庆一中寄宿学校2015年对校园进行扩建．某天一台塔吊正对新建教学楼进行封顶施工，工人在楼顶A处测得吊钩D处的俯角α=22°，测得塔吊B，C两点的仰角分别为β=27°，γ=50°，此时B与C距3米，塔吊需向A处吊运材料．（tan27°≈0.5，tan50°≈1.2，tan22°≈0.4）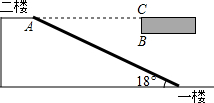
如图，某大型商场在一楼至二楼之间安装有电梯，二楼地板厚BC为0.24米，AC=7米．
若b是最小的正整数，且a、b满足（c-5）2+|a+b|=0．