题目内容
12.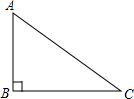 如图,在Rt△ABC中,∠C=90°,AC=6,AB=3,求∠C的三个三角函数值.
如图,在Rt△ABC中,∠C=90°,AC=6,AB=3,求∠C的三个三角函数值.
分析 先利用勾股定理计算出BC=3$\sqrt{3}$,然后根据锐角三角函数的定义求解.
解答 解:∵∠B=90°,AC=6,AB=3,
∴BC=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∵sinC=$\frac{AB}{AC}$=$\frac{3}{6}$=$\frac{1}{2}$,
cosC=$\frac{BC}{AC}$=$\frac{3\sqrt{3}}{6}$=$\frac{\sqrt{3}}{2}$,
tanC=$\frac{AB}{BC}$=$\frac{3}{3\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活应用勾股定理和锐角三角函数的定义.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
16.矩形两对角线交角为60°,且一条对角线与最短边的和为10,则对角线的长是( )
| A. | $\frac{10}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{25}{3}$ |
2.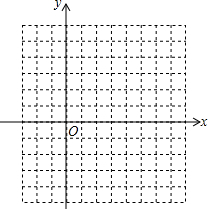 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.
(1)将抛物线的解析式化为顶点式.
(2)在坐标系中利用五点法画出此抛物线.
(3)结合图象,当0<x<3时,y的取值范围-1≤y<3.
 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.(1)将抛物线的解析式化为顶点式.
(2)在坐标系中利用五点法画出此抛物线.
| x | … | … | |||||
| y | … | … |
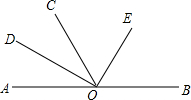 如图,O为直线AB上一点,∠A0D=∠COD,∠COE=∠EOB,若∠DOC:∠COE=2:3,求∠DOE,∠COD与∠COE的度数.
如图,O为直线AB上一点,∠A0D=∠COD,∠COE=∠EOB,若∠DOC:∠COE=2:3,求∠DOE,∠COD与∠COE的度数.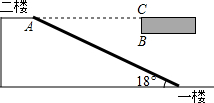 如图,某大型商场在一楼至二楼之间安装有电梯,二楼地板厚BC为0.24米,AC=7米.
如图,某大型商场在一楼至二楼之间安装有电梯,二楼地板厚BC为0.24米,AC=7米.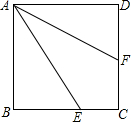 如图,已知正方形ABCD,点E在BC上,BE=2EC,点F在CD上,∠EAF=30°,求$\frac{CF}{DF}$.
如图,已知正方形ABCD,点E在BC上,BE=2EC,点F在CD上,∠EAF=30°,求$\frac{CF}{DF}$.