题目内容
8. 如图,在Rt△ABC中,已知∠C=90°,BC=5,AB=5$\sqrt{2}$,求∠A、∠B及AC的值.
如图,在Rt△ABC中,已知∠C=90°,BC=5,AB=5$\sqrt{2}$,求∠A、∠B及AC的值.
分析 在Rt△ACB中,∠C=90°,BC=5,AB=5$\sqrt{2}$,根据sinA=$\frac{BC}{AB}=\frac{5}{5\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,求得∠A=45°,根据三角形的内角和得到∠B=90°-45°=45°,于是得到结论.
解答 解:∵在Rt△ACB中,∠C=90°,BC=5,AB=5$\sqrt{2}$,
∴sinA=$\frac{BC}{AB}=\frac{5}{5\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴∠A=45°,
∴∠B=90°-45°=45°,
∴AC=BC=5.
点评 本题考查了解直角三角形和特殊角的三角函数的应用,能灵活运用锐角三角形函数的定义进行计算是解此题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
12.琥珀中学开展“节约用电,低碳生活”活动,为了了解开展活动一个月以来节约用电的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月的节电情况,如表:
请你估计这20名同学的家庭一个月节约用电的平均数是( )
| 节电量(度) | 20 | 25 | 30 | 40 | 50 |
| 家庭数(个) | 2 | 4 | 6 | 7 | 1 |
| A. | 30度 | B. | 32.5度 | C. | 33度 | D. | 34度 |
 为了给学生提供更好的学习生活环境,重庆一中寄宿学校2015年对校园进行扩建.某天一台塔吊正对新建教学楼进行封顶施工,工人在楼顶A处测得吊钩D处的俯角α=22°,测得塔吊B,C两点的仰角分别为β=27°,γ=50°,此时B与C距3米,塔吊需向A处吊运材料.(tan27°≈0.5,tan50°≈1.2,tan22°≈0.4)
为了给学生提供更好的学习生活环境,重庆一中寄宿学校2015年对校园进行扩建.某天一台塔吊正对新建教学楼进行封顶施工,工人在楼顶A处测得吊钩D处的俯角α=22°,测得塔吊B,C两点的仰角分别为β=27°,γ=50°,此时B与C距3米,塔吊需向A处吊运材料.(tan27°≈0.5,tan50°≈1.2,tan22°≈0.4)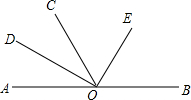 如图,O为直线AB上一点,∠A0D=∠COD,∠COE=∠EOB,若∠DOC:∠COE=2:3,求∠DOE,∠COD与∠COE的度数.
如图,O为直线AB上一点,∠A0D=∠COD,∠COE=∠EOB,若∠DOC:∠COE=2:3,求∠DOE,∠COD与∠COE的度数.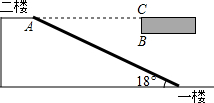 如图,某大型商场在一楼至二楼之间安装有电梯,二楼地板厚BC为0.24米,AC=7米.
如图,某大型商场在一楼至二楼之间安装有电梯,二楼地板厚BC为0.24米,AC=7米.