题目内容
20.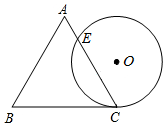 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1.5cm |
分析 连接OC,并过点O作OF⊥CE于F,求出等边三角形的高即可得出圆的直径,继而得出OC的长度,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
解答  解:连接OC,并过点O作OF⊥CE于F,
解:连接OC,并过点O作OF⊥CE于F,
∵△ABC为等边三角形,边长为4cm,
∴△ABC的高为2$\sqrt{3}$cm,
∴OC=$\sqrt{3}$cm,
又∵∠ACB=60°,
∴∠OCF=30°,
在Rt△OFC中,可得FC=$\frac{3}{2}$cm,
即CE=2FC=3cm.
故选B.
点评 本题主要考查了切线的性质,等边三角形的性质和解直角三角形的有关知识,题目不是太难,属于基础性题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.一个多边形的内角和是外角和的2倍,这个多边形的边数为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
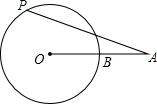 如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是30°.
如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是30°.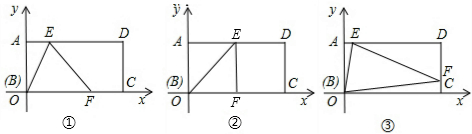
 如图是由6个相同的小正方体组成的几何体,那么这个几何体的俯视图是( )
如图是由6个相同的小正方体组成的几何体,那么这个几何体的俯视图是( )



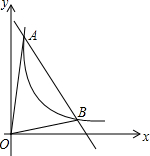 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.