题目内容
5.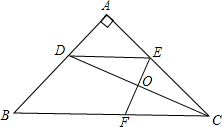 如图,在△ABC中,AB=AC,∠A=90°,CD平分∠ACB,E在AC上,且AE=AD,EF⊥CD交BC于点F,交CD于点O.求证:BF=2AD.
如图,在△ABC中,AB=AC,∠A=90°,CD平分∠ACB,E在AC上,且AE=AD,EF⊥CD交BC于点F,交CD于点O.求证:BF=2AD.
分析 连接DF,证明四边形CEDF是平行四边形,再证出四边形CEDF为菱形,得出DF∥CE,DF=CE=CF=DE,由等腰直角三角形的性质得出BF=$\sqrt{2}$DF,DE=$\sqrt{2}$AD,即可得出结论.
解答 证明:连接DF,如图所示:
∵AD=AE,AB=AC,
∴AD:AB=AE:AC,
∴DE∥BC,
∴∠CDE=∠BCD,
∵CD平分∠ACB,
∴∠BCD=∠DCE,
∴DE=CE,
∵EF⊥CD,
∴OD=OC,
∵DE∥CF,
∴OE=OF,
∴四边形CEDF是平行四边形,
∴四边形CEDF为菱形,
∴DF∥CE,DF=CE=CF=DE,
∵∠A=90°,AB=AC,
∴DF⊥AB,∠B=45°,
∴BF=$\sqrt{2}$DF,
∵AD=AE,∠A=90°,
∴DE=$\sqrt{2}$AD,
∴BF=$\sqrt{2}$×$\sqrt{2}$AD=2AD.
点评 本题考查了平行四边形的判定与性质、菱形的判定与性质、等腰直角三角形的性质;熟练掌握等腰直角三角形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
 已知:如图,AB=CD,AB∥CD,FD∥EB 求证:CE=AF.
已知:如图,AB=CD,AB∥CD,FD∥EB 求证:CE=AF.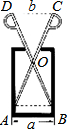 如图,质地均匀的空心圆柱形零件的外直径为a,现用一个交叉钳(AC和BD的长相等)测量,如果$\frac{OA}{OC}=\frac{OB}{OD}=n$,而且CD=b,那么这个零件的厚度为$\frac{a-bn}{2}$.
如图,质地均匀的空心圆柱形零件的外直径为a,现用一个交叉钳(AC和BD的长相等)测量,如果$\frac{OA}{OC}=\frac{OB}{OD}=n$,而且CD=b,那么这个零件的厚度为$\frac{a-bn}{2}$.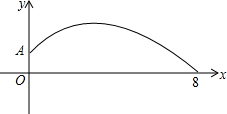 某学校在一次投掷铅球时,刚出手时铅球离地面$\frac{5}{3}$m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图所示:
某学校在一次投掷铅球时,刚出手时铅球离地面$\frac{5}{3}$m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图所示: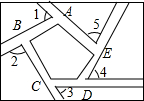 清晨,小强沿着一个五边形广场周围的小路,按逆时针方向跑步.
清晨,小强沿着一个五边形广场周围的小路,按逆时针方向跑步. 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数.