题目内容
16．
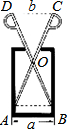如图，质地均匀的空心圆柱形零件的外直径为a，现用一个交叉钳（AC和BD的长相等）测量，如果$\frac{OA}{OC}=\frac{OB}{OD}=n$，而且CD=b，那么这个零件的厚度为$\frac{a-bn}{2}$．
分析 利用已知可得出△DOC∽△BOA，再利用相似三角形的性质得出AB的值，进而得出答案．
解答 解：∵$\frac{OA}{OC}=\frac{OB}{OD}=n$，∠DOC=∠AOB，
∴△DOC∽△BOA，
∴$\frac{OA}{OC}=\frac{OB}{DO}$=$\frac{AB}{DC}$=n，
∵DC=b，
∴AB=bn，
∴这个零件的厚度为：$\frac{a-bn}{2}$．
故答案为：$\frac{a-bn}{2}$．
点评 此题主要考查了相似三角形的应用，根据题意表示出AB的长是解题关键．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
11．化简二次根式$\sqrt{-\frac{1}{x}}$（x＜0），得（ ）
| A． | $\frac{{\sqrt{x}}}{x}$ | B． | $\frac{{\sqrt{-x}}}{x}$ | C． | $-\frac{{\sqrt{-x}}}{x}$ | D． | $-\frac{{\sqrt{x}}}{x}$ |
1．若分式$\frac{3x}{x-1}$有意义，则x应满足（ ）
| A． | x=0 | B． | x≠0 | C． | x≠1 | D． | x=1 |
8．相交两圆的圆心距是5cm，其中一圆半径是3cm，则另一圆的半径可能是（ ）
| A． | 1cm | B． | 8cm | C． | 4cm | D． | 2cm |
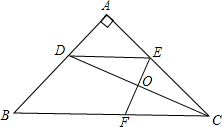如图，在△ABC中，AB=AC，∠A=90°，CD平分∠ACB，E在AC上，且AE=AD，EF⊥CD交BC于点F，交CD于点O．求证：BF=2AD．