题目内容
12.解方程x2-x-1=0的两个实根为a,b,求$\frac{a}{b(a-b)}-\frac{b}{a(a-b)}$的值.分析 先化简$\frac{a}{b(a-b)}-\frac{b}{a(a-b)}$,再根据根与系数的关系得出a+b和ab的值,代入计算即可.
解答 解:∵a,b是方程x2-x-1=0的两个实根,
∴a+b=1,ab=-1,
∴$\frac{a}{b(a-b)}-\frac{b}{a(a-b)}$=$\frac{{a}^{2}-{b}^{2}}{ab(a-b)}$
=$\frac{(a+b)(a-b)}{ab(a-b)}$
=$\frac{a+b}{ab}$
=$\frac{1}{-1}$
=-1.
点评 本题考查了根与系数的关系以及分式的化简求值,把分式化简是解题的关键.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
17.下列运算正确的是( )
| A. | (-p2q)3=-p5q3 | B. | (12a2b3c)÷(6ab2)=2ab | ||
| C. | (x2-4x)x-1=x-4 | D. | 3m2÷(3m-1)=m-3m2 |
4.下列各运算中,正确的是( )
| A. | a2+a3=a5 | B. | (a+1)2=a2+1 | C. | $\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$ | D. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
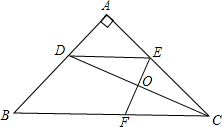 如图,在△ABC中,AB=AC,∠A=90°,CD平分∠ACB,E在AC上,且AE=AD,EF⊥CD交BC于点F,交CD于点O.求证:BF=2AD.
如图,在△ABC中,AB=AC,∠A=90°,CD平分∠ACB,E在AC上,且AE=AD,EF⊥CD交BC于点F,交CD于点O.求证:BF=2AD.
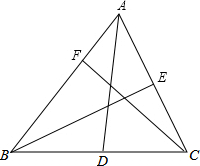 如图,在△ABC中,
如图,在△ABC中,