题目内容
18.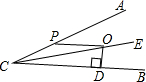 已知∠ACB的角平分线CE,O是CE上一点,OP∥BC,PO=2,OD⊥CB于D,∠ACE=15°,则OD的长是( )
已知∠ACB的角平分线CE,O是CE上一点,OP∥BC,PO=2,OD⊥CB于D,∠ACE=15°,则OD的长是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
分析 作OF⊥AC于F,根据角平分线的定义求出∠AOB的度数,根据平行线的性质求出∠APO的度数,根据直角三角形的性质求出OF,根据角平分线的性质求出答案.
解答 解: 作OF⊥AC于F,
作OF⊥AC于F,
∵CE是∠ACB的角平分线,∠ACE=15°,
∴∠AOB=2∠ACE=30°,
∵OP∥BC,
∴∠APO=∠AOB=30°,
∴OF=$\frac{1}{2}$PO=1,
∵CE是∠ACB的角平分线,OF⊥AC,OD⊥CB,
∴OD=OF=1,
故选:B.
点评 本题考查的是角平分线的性质、直角三角形的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
8.下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差S2:
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择甲.
| 甲 | 乙 | 丙 | 丁 | |
| 平均数x(cm) | 175 | 173 | 175 | 174 |
| 方差S2(cm2) | 3.5 | 3.5 | 12.5 | 15 |
 如图,某校九年级课外活动小组,在测量树高的一次活动中,测得树底部中心A到斜坡底C的水平距离为8m,在阳光下某一时刻测得1m场的标杆影长是0.5m,同时树影落在斜坡上的部分CD=4m,已知斜坡CD的坡比i=1:$\sqrt{3}$,求树高AB.(结果保留根号)
如图,某校九年级课外活动小组,在测量树高的一次活动中,测得树底部中心A到斜坡底C的水平距离为8m,在阳光下某一时刻测得1m场的标杆影长是0.5m,同时树影落在斜坡上的部分CD=4m,已知斜坡CD的坡比i=1:$\sqrt{3}$,求树高AB.(结果保留根号)
 如图所示,每个小正方形的变成都是1厘米,现有一半径为1厘米的圆沿着图形内测运动,如果此圆作旋转(无滑动的滚动)运动,则它经过部分的面积是(34+$\frac{7}{2}π$)平方厘米.(答案保留π)
如图所示,每个小正方形的变成都是1厘米,现有一半径为1厘米的圆沿着图形内测运动,如果此圆作旋转(无滑动的滚动)运动,则它经过部分的面积是(34+$\frac{7}{2}π$)平方厘米.(答案保留π)