题目内容

10．一个多边形的每一个外角都等于40°，则该多边形的内角和等于1260°．

分析 先利用360°÷40°求出多边形的边数，再根据多边形的内角和公式（n-2）•180°计算即可求解．

解答 解：多边形的边数是：360°÷40°=9，
则内角和是：（9-2）•180°=1260°．
故答案是：1260°．

点评 本题主要考查了正多边形的外角与边数的关系，求出多边形的边数是解题的关键．

练习册系列答案
相关题目
5．计算：
（1）|-3|+（$\root{3}{27}$-1）0-$\sqrt{16}$+（$\frac{1}{3}$）-1
（2）（$\sqrt{5}-1$）2+$\sqrt{20}$-$\sqrt{40}$$÷\sqrt{8}$．
1．如图（a）所示直角三角板ABC的边长BC=a，AC=b，开始时AB边靠在y轴上，B与坐标原点O重合．今使A点沿y轴负方向朝O点移动，B点沿x轴正方向移动，可知三角板从图（a）所示的初始位置到图（b）所示终止位置的过程中，C点的运动轨迹为往返的直线（选填：“单方向的直线“、“往返的直线“、“一段圆弧“或“非圆弧状的其他曲线“），C点在此过程中通过的路程为2$\sqrt{{a}^{2}+{b}^{2}}$-a-b．
18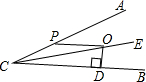．已知∠ACB的角平分线CE，O是CE上一点，OP∥BC，PO=2，OD⊥CB于D，∠ACE=15°，则OD的长是（　　）
A．$\frac{1}{2}$B．1C．2D．3
5．某公司销售部有营销人员15人，销售部为了制定某种商品的月销售额，统计了这15人某月的销售量如表所示：
每人销售件数1201502102505201800
 人数 2 3 5 3 1 1
（1）求这15位营销人员该月销售量的平均数；
（2）销售量为150件的频率为多少？
15．以下列各组长度的线段为三边，能构成直角三角形的是（　　）
A．2，3，4B．4，5，6C．1，$\sqrt{2}$，$\sqrt{3}$D．2，$\sqrt{3}$，$\sqrt{5}$
2．一件商品降价10%后的价格为x元，那么这件商品的原价为（　　）
A．（x+10%）元B．x（1+10%）元C．$\frac{x}{1-10%}$元D．$\frac{x}{1+10%}$元
19．运算（-mn2）3的结果是（　　）
A．-m3n5B．m3n6C．-m3n6D．m3n5
20．108°35′的补角是71°25′．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网