题目内容
用配方法将下列函数化成y=a(x+h)2+k的形式,并指出抛物线的开口方向,对称轴和顶点坐标.
(1)y=-
x2+6x-17;
(2)y=(2-x)(1+2x).
(1)y=-
| 1 |
| 2 |
(2)y=(2-x)(1+2x).
考点:二次函数的三种形式
专题:
分析:(1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式;
(2)化为一般式后,利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
(2)化为一般式后,利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
解答:解:(1)y=-
x2+6x-17=-
(x2-12x+36)+18-17=-
(x-6)2+1,
∵a=-
<0,
∴开口向下,
对称轴为直线x=6,顶点坐标为(6,1);
(2)y=(2-x)(1+2x)=-2x2+3x+2=-2(x2-
x+
)+
+2=-2(x-
)2+
,
∵a=-2<0,
∴开口向下,
对称轴为直线x=
,顶点坐标为(
,
).
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵a=-
| 1 |
| 2 |
∴开口向下,
对称轴为直线x=6,顶点坐标为(6,1);
(2)y=(2-x)(1+2x)=-2x2+3x+2=-2(x2-
| 3 |
| 2 |
| 9 |
| 16 |
| 9 |
| 8 |
| 3 |
| 4 |
| 25 |
| 8 |
∵a=-2<0,
∴开口向下,
对称轴为直线x=
| 3 |
| 4 |
| 3 |
| 4 |
| 25 |
| 8 |
点评:本题考查了二次函数的解析式的三种形式:(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;(3)交点式(与x轴):y=a(x-x1)(x-x2).同时考查了二次函数的性质.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
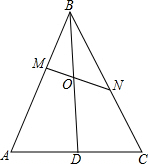 已知在△ABC中,
已知在△ABC中,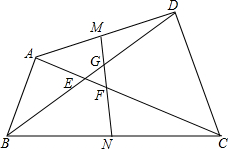 如图,BD=AC,M、N分别为AD、BC的中点,AC、BD交于E,MN与BD、AC分别交于点F、G,求证:EF=EG.
如图,BD=AC,M、N分别为AD、BC的中点,AC、BD交于E,MN与BD、AC分别交于点F、G,求证:EF=EG. 如图,已知l是第一、三象限的角平分线,点P与P′关于l对称,已知点P的坐标为(a,b),猜想P′的坐标是什么?并说明你猜想的正确性.
如图,已知l是第一、三象限的角平分线,点P与P′关于l对称,已知点P的坐标为(a,b),猜想P′的坐标是什么?并说明你猜想的正确性.