题目内容
15. 如图,菱形ABCD的边长为6,BD=6,E、F分别是边AD、CD上的两个动点,且满足AE+CF=6.
如图,菱形ABCD的边长为6,BD=6,E、F分别是边AD、CD上的两个动点,且满足AE+CF=6.(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)设△BEF的周长为m,求m的取值范围.
分析 (1)根据菱形对角线平分且垂直的性质,求得BD;
(2)先证明△OCE≌△ODE,得DE=DF,∠ADE=∠BDF,从而得到∴△DEF是等边三角形;
(3)先确定条件,即当DE⊥AB时,DE最短,此时△DEF的周长最短,当E点与A点或B点重合时,BE最长,分别求出m的值即可;
解答 解:(1)∵四边形ABCD是菱形,
∴AB=CB=CD=DA=6,
∵BD=6,
∴△ABD,△BDC都是等边三角形,
∵AE+CF=6,AE+DE=6,
∴DE=CF,
在△BDE和△BCF中,
$\left\{\begin{array}{l}{ED=FC}\\{BD=BC}\\{∠BDE=∠BCF=60°}\end{array}\right.$,
∴△BDE≌△CBF.
(2)结论:△BEF是等边三角形.
理由:由(1)可知,BE=BF,∠EBD=∠FBC,
∵∠DBF+FBC=60°,
∴∠EBD+∠DBF=60°,
∴∠EBF=60°,
∴△EBF是等边三角形.
(3)当BE⊥AD时,BE最短,此时BE=3$\sqrt{3}$,m=3BE=9$\sqrt{3}$,
当E点与A点或B点重合时,BE最长,此时BE=6,m=3BE=18,
∴m的取值范围为:9$\sqrt{3}$≤m≤18.
点评 本题是菱形的性质、等边三角形的判定和性质、全等三角形的判定和性质,垂线段最短等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
5.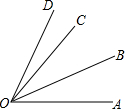 如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
 如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )| A. | 70° | B. | 83° | C. | 68° | D. | 85° |
6. 某中学八年级的八(一)班、八(二)班分别选5名同学参加“文明创建”知识大赛活动,其预赛成绩如图所示:
某中学八年级的八(一)班、八(二)班分别选5名同学参加“文明创建”知识大赛活动,其预赛成绩如图所示:
(1)根据如图,填写下表.
(2)请从不同的角度对两班的成绩进行分析评价(至少写出三条);
(3)八(二)班选手飞飞说:“我的成绩是中等水平,”你知道他是几号选手吗?请简述理由.
 某中学八年级的八(一)班、八(二)班分别选5名同学参加“文明创建”知识大赛活动,其预赛成绩如图所示:
某中学八年级的八(一)班、八(二)班分别选5名同学参加“文明创建”知识大赛活动,其预赛成绩如图所示:(1)根据如图,填写下表.
| 平均数 | 中位数 | 众数 | 方差 | |
| 八(一)班 | 8.5 | 8.5 | 8.5 | 0.7 |
| 八(二)班 | 8.5 | 8 | 10 | 1.6 |
(3)八(二)班选手飞飞说:“我的成绩是中等水平,”你知道他是几号选手吗?请简述理由.

 如图,P是等边三角形ABC内的一点,将△PAC绕点A逆时针旋转得到△P′AC′,若点C′与点B重合,则∠PAP′的大小为60度.
如图,P是等边三角形ABC内的一点,将△PAC绕点A逆时针旋转得到△P′AC′,若点C′与点B重合,则∠PAP′的大小为60度.