题目内容
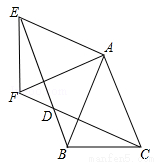
2.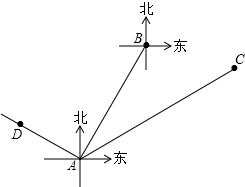 如图,在某海域内有A,C两个港口,港口C在港口A北偏东60°方向上,一艘船以每小时36海里的速度沿北偏东30°的方向驶离A港口,3小时后到达B点位置,在B处测得港口C在B处的南偏东75°方向上,求B处离港口C有多少海里.(结果保留根号)
如图,在某海域内有A,C两个港口,港口C在港口A北偏东60°方向上,一艘船以每小时36海里的速度沿北偏东30°的方向驶离A港口,3小时后到达B点位置,在B处测得港口C在B处的南偏东75°方向上,求B处离港口C有多少海里.(结果保留根号)
分析 如图作BM⊥AC于M,首先证明∠C=45°,分别在RT△ABM和RT△MBC中求出BM、BC即可解决问题.
解答 解:如图作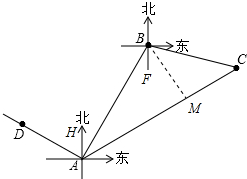 BM⊥AC于M,
BM⊥AC于M,
∵∠HAC=60°,∠HAB=30°,
∴∠BAC=30°,
∵AH∥BF,
∴∠ABF=∠HAF=30°,
∵∠FBC=75°,
∴∠ABC=∠ABF+∠FBC=105°,
∴∠C=180°-∠BAC-∠ABC=45°,
∵∠BMC=90°,
∴∠MBC=∠MCB=45°,
∴MB=MC,
在RT△ABM中,∠AMB=90°,AB=36×3=108海里,∠BAM=30°,
∴BM=$\frac{1}{2}$AB=54,
∴BC=$\sqrt{2}$BM=54$\sqrt{2}$海里.
答:B处离港口C有54$\sqrt{2}$海里.
点评 本题考查解直角三角形、方向角、三角函数、特殊角的三角函数值等知识,添加辅助线构造直角三角形是解题的关键,把一般三角形转化为特殊三角形解决,属于中考常考题型.

练习册系列答案
相关题目
6.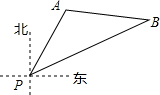 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔20海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的北偏东60°方向上的B处,则此时轮船与灯塔的距离BP为20$\sqrt{3}$海里.
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔20海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的北偏东60°方向上的B处,则此时轮船与灯塔的距离BP为20$\sqrt{3}$海里.
 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔20海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的北偏东60°方向上的B处,则此时轮船与灯塔的距离BP为20$\sqrt{3}$海里.
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔20海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的北偏东60°方向上的B处,则此时轮船与灯塔的距离BP为20$\sqrt{3}$海里.
10.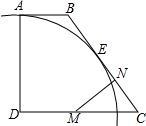 如图,四边形ABCD中∠D=90°,以点D为圆心,AD为半径作⊙D,AB和BC分别切⊙D于点A和点E,若AB=4,DC=10,点M、N分别在线段DC、BC上,且MN=DM,则DM的最小值为( )
如图,四边形ABCD中∠D=90°,以点D为圆心,AD为半径作⊙D,AB和BC分别切⊙D于点A和点E,若AB=4,DC=10,点M、N分别在线段DC、BC上,且MN=DM,则DM的最小值为( )
 如图,四边形ABCD中∠D=90°,以点D为圆心,AD为半径作⊙D,AB和BC分别切⊙D于点A和点E,若AB=4,DC=10,点M、N分别在线段DC、BC上,且MN=DM,则DM的最小值为( )
如图,四边形ABCD中∠D=90°,以点D为圆心,AD为半径作⊙D,AB和BC分别切⊙D于点A和点E,若AB=4,DC=10,点M、N分别在线段DC、BC上,且MN=DM,则DM的最小值为( )| A. | 5 | B. | 6 | C. | 5.5 | D. | $\frac{40}{9}$ |
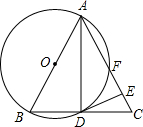 如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点F,过点D作⊙O的切线交AC于E.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点F,过点D作⊙O的切线交AC于E.