题目内容
20. 如图,AB∥EF,BC∥FG,BM、FN分别是∠ABC、∠EFG的三等分线且靠近AB、EF,求证:BM∥FN.
如图,AB∥EF,BC∥FG,BM、FN分别是∠ABC、∠EFG的三等分线且靠近AB、EF,求证:BM∥FN.
分析 如图,设FN交BC于O,根据平行线的性质可得∠ABC=∠EHC,在△HOF中结合外角的性质可得到∠EHO=∠2+∠HOF,可证明∠MBC=HOF,可证明BM∥FN.
解答  证明:
证明:
如图,设FN交BC于点O,
∵AB∥EF,
∴∠ABC=∠EHO,
又∠ABC=∠1+∠MBC,∠EHO=∠2+∠HOF,
∴∠1+∠MBC=∠2+∠HOF,
∵∠1=∠2,
∴∠MBC=∠HOF,
∴BM∥FN.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
11.方程x2=2x的解是( )
| A. | x=2 | B. | x1=2,x2=0 | C. | x1=$\sqrt{2}$,x2=0 | D. | x=0 |
9.地球上的海洋面积约为36100000km2,用科学记数法可表示为( )
| A. | 3.61×106km2 | B. | 3.61×107km2 | C. | 0.361×108km2 | D. | 3.61×109km2 |
 如图,已知DE∥BC,EF平分∠DEC,且∠ADE=50°,∠C=80°.
如图,已知DE∥BC,EF平分∠DEC,且∠ADE=50°,∠C=80°. 在三角形ABC中,∠B=90°,D在AC边上,DF⊥BC于F,DE⊥AB于E,则线段AB与DF平行吗?BC与DE平行吗?为什么.
在三角形ABC中,∠B=90°,D在AC边上,DF⊥BC于F,DE⊥AB于E,则线段AB与DF平行吗?BC与DE平行吗?为什么.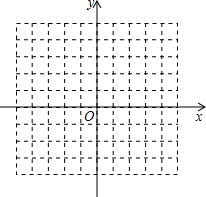 如图,已知A(-3,-3),B(-2,-1),C(-1,-3)是直角坐标平面上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1,-3)是直角坐标平面上三点. 如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=120°,BE=2,FD=3,则∠EAF=60°,?ABCD的周长为20.
如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=120°,BE=2,FD=3,则∠EAF=60°,?ABCD的周长为20.