题目内容
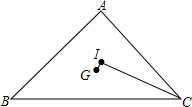 如图,△ABC的三边长BC=a,CA=b,AB=c,a、b、c都是整数,且a、b的最大公约数为2.点G和点I分别为△ABC的重心和内心,且∠GIC=90°.求△ABC的周长.
如图,△ABC的三边长BC=a,CA=b,AB=c,a、b、c都是整数,且a、b的最大公约数为2.点G和点I分别为△ABC的重心和内心,且∠GIC=90°.求△ABC的周长.考点:三角形的五心
专题:
分析:延长GI分别交BC于点P,AC于点Q,首先证明△CPQ为等腰三角形,根据内心和重心的知识分别表示出△PCQ的面积,进而求出a,b,c之间的等量关系式,最后对a,b,c进行讨论,进而求出a,b和c的值.
解答: 解:延长GI分别交BC于点P,AC于点Q,
解:延长GI分别交BC于点P,AC于点Q,
∵∠GIC=90°,
∴GI⊥CI,I是内心,
∴△CPQ为等腰三角形,
∴PC=QC,
∴S△PCQ=2S△CQI=r×CQ(r为三角形ABC内切圆半径)
∴S△PCQ=S△PGC+S△CGQ,
=
PC•ha(ha为GE⊥BC的高)+
CQ•hb(hb为GF⊥AC的高)
=
CQ(ha+hb)=r×CQ
∴2r=ha+hb①
∵r=
②
∵S△ABC=
×a•ha'(ha'为AM⊥BC的高)=
×a•ha,
∴ha=
,hb=
,
∴ha+hb=
+
③
把②③代入①得
=
,
当a=2,b=2时,c=2,
∵△ABC为等边三角形,
∴GI重合,舍去,
∴a≠b,
设a>b,a=2m,b=2n,
∵a、b的最大公约数为2,
∴(m,n)=1,
∴m+n整除12,
即m=7,n=5,
∴a=14,b=10,c=11,
∴a+b+c=35.
 解:延长GI分别交BC于点P,AC于点Q,
解:延长GI分别交BC于点P,AC于点Q,∵∠GIC=90°,
∴GI⊥CI,I是内心,
∴△CPQ为等腰三角形,
∴PC=QC,
∴S△PCQ=2S△CQI=r×CQ(r为三角形ABC内切圆半径)
∴S△PCQ=S△PGC+S△CGQ,
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
∴2r=ha+hb①
∵r=
| 2S△ABC |
| a+b+c |
∵S△ABC=
| 1 |
| 2 |
| 3 |
| 2 |
∴ha=
| 2S△ABC |
| 3a |
| 2S△ABC |
| 3b |
∴ha+hb=
| 2S△ABC |
| 3a |
| 2S△ABC |
| 3b |
把②③代入①得
| 6 |
| a+b+c |
| a+b |
| ab |
当a=2,b=2时,c=2,
∵△ABC为等边三角形,
∴GI重合,舍去,
∴a≠b,
设a>b,a=2m,b=2n,
∵a、b的最大公约数为2,
∴(m,n)=1,
∴m+n整除12,
即m=7,n=5,
∴a=14,b=10,c=11,
∴a+b+c=35.
点评:本题主要考查了三角形五心的知识点,解答本题的关键是要熟练掌握内心和重心的定义以及三角形面积与内切圆半径和三边长的关系式,此题有一定的难度.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
化简|-2014|等于( )
| A、2014 |
| B、-2014 |
| C、±2 014 |
| D、-2013 |
 如图,山脚下有A、B两点,用两种方法测量A、B两点间的距离.
如图,山脚下有A、B两点,用两种方法测量A、B两点间的距离. 如图,平面直角坐标系中,直线
如图,平面直角坐标系中,直线 如图:已知四边形ABCD是平行四边形,DE⊥AB于点E,点M为BC的中点,BC=2AB,∠BEM=50°,求∠B的度数.
如图:已知四边形ABCD是平行四边形,DE⊥AB于点E,点M为BC的中点,BC=2AB,∠BEM=50°,求∠B的度数.