题目内容
阅读理解并解答
为了求1+2+22+23+24+…+22009的值，可令S=1+2+22+23+24+…+22009则2S=2+22+23+24+…+22009+22010，因此：2S-S=（2+22+23+24+…+22009+22010）-（1+2+22+23+24+…+22009）=22010-1．
所以：S=22010-1． 即1+2+22+23+24+…+22009=22010-1．
（1）请依照上面的方法，求1+3+32+33+34+…+32012的值．
（2）a+a2+a3+a4+…+a2012（a≠1）= （直接填写结果）．
为了求1+2+22+23+24+…+22009的值，可令S=1+2+22+23+24+…+22009则2S=2+22+23+24+…+22009+22010，因此：2S-S=（2+22+23+24+…+22009+22010）-（1+2+22+23+24+…+22009）=22010-1．
所以：S=22010-1． 即1+2+22+23+24+…+22009=22010-1．
（1）请依照上面的方法，求1+3+32+33+34+…+32012的值．
（2）a+a2+a3+a4+…+a2012（a≠1）=
考点：整式的混合运算
专题：阅读型
分析：（1）设S=1+3+32+33+34+…+32012，则3S=3+32+33+34+…+32012+32013，两式相减即可求出答案；
（2）设S=a+a2+a3+a4+…+a2012，再两边都乘以a，最后相减，即可求出答案．
（2）设S=a+a2+a3+a4+…+a2012，再两边都乘以a，最后相减，即可求出答案．
解答：解：（1）∵设S=1+3+32+33+34+…+32012，
则3S=3+32+33+34+…+32012+32013，
∴2S=32013-1，
S=
，
即1+3+32+33+34+…+32012=
；
（2）a+a2+a3+a4+…+a2012（a≠1）=
．
故答案为：
．
则3S=3+32+33+34+…+32012+32013，
∴2S=32013-1，
S=
| 22013-1 |
| 2 |
即1+3+32+33+34+…+32012=
| 22013-1 |
| 2 |
（2）a+a2+a3+a4+…+a2012（a≠1）=
| a2013-a |
| a-1 |
故答案为：
| a2013-a |
| a-1 |
点评：本题考查了整式的混合运算和求值的应用，主要考查学生的理解能力和计算能力，题目比较好，有一定的难度．
练习册系列答案
相关题目
以下列各组线段为边，能组成三角形的是（ ）
| A、4cm，4cm，8cm |
| B、1cm，5cm，6cm |
| C、7cm，5cm，3cm |
| D、10cm，2cm，7cm |
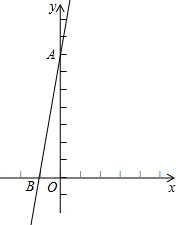如图，在直角坐标系xOy中，直线y=7x+7交x轴于B，交y轴于A．
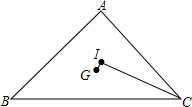如图，△ABC的三边长BC=a，CA=b，AB=c，a、b、c都是整数，且a、b的最大公约数为2．点G和点I分别为△ABC的重心和内心，且∠GIC=90°．求△ABC的周长．