题目内容
假若有两边和一角对应相等的两个三角形,请证明:
(1)若这两个三角形都是锐角三角形,则这两个三角形全等;
(2)若这个角的对边恰好是这两边中的大边,则这两个三角形全等.
(1)若这两个三角形都是锐角三角形,则这两个三角形全等;
(2)若这个角的对边恰好是这两边中的大边,则这两个三角形全等.
考点:全等三角形的判定
专题:证明题
分析:(1)根据已知可得出△ABC和△DEF的形状已经确定,即AC与DF的长已经确定,进而求出即可;
(2)根据已知可得出△ABC和△DEF的形状已经确定,即AC与DF的长已经确定,进而求出即可.
(2)根据已知可得出△ABC和△DEF的形状已经确定,即AC与DF的长已经确定,进而求出即可.
解答: 证明:(1)如图1:∵这两个三角形都是锐角三角形,当∠C=∠F,AB=DE,BC=EF,
证明:(1)如图1:∵这两个三角形都是锐角三角形,当∠C=∠F,AB=DE,BC=EF,
∴△ABC和△DEF的形状已经确定,即AC与DF的长已经确定,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SSS);
(2)如图1:∵这个角的对边恰好是这两边中的大边,当∠A=∠D,AB=DE,BC=EF,
∴△ABC和△DEF的形状已经确定,即AC与DF的长已经确定,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
 证明:(1)如图1:∵这两个三角形都是锐角三角形,当∠C=∠F,AB=DE,BC=EF,
证明:(1)如图1:∵这两个三角形都是锐角三角形,当∠C=∠F,AB=DE,BC=EF,∴△ABC和△DEF的形状已经确定,即AC与DF的长已经确定,
在△ABC和△DEF中
|
∴△ABC≌△DEF(SSS);
(2)如图1:∵这个角的对边恰好是这两边中的大边,当∠A=∠D,AB=DE,BC=EF,
∴△ABC和△DEF的形状已经确定,即AC与DF的长已经确定,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SSS).
点评:此题主要考查了全等三角形的判定,根据已知画出图形,进而确定三角形的形状是解题关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
22004(
)-2(
)1002=( )
| 3 |
| 2 |
| 1 |
| 4 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
一直角三角形的斜边长为10,一直角边长为6,则另一直角长为( )
| A、4 | B、8 | C、10 | D、12 |
已知:直线y=-
x+
(n为正整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2014=( )
| n |
| n+1 |
| 1 |
| n+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
-
的相反数是( )
| 5 |
| 8 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
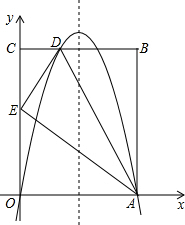 如图,在直角坐标系中,A点在x轴上,AB∥y轴,C点在y轴上,CB∥x轴,点B的坐标为(8,10),点D在BC上,将△ABD沿直线AD翻折,使得点B刚好落在y轴的点E处.
如图,在直角坐标系中,A点在x轴上,AB∥y轴,C点在y轴上,CB∥x轴,点B的坐标为(8,10),点D在BC上,将△ABD沿直线AD翻折,使得点B刚好落在y轴的点E处.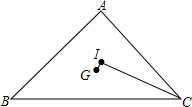 如图,△ABC的三边长BC=a,CA=b,AB=c,a、b、c都是整数,且a、b的最大公约数为2.点G和点I分别为△ABC的重心和内心,且∠GIC=90°.求△ABC的周长.
如图,△ABC的三边长BC=a,CA=b,AB=c,a、b、c都是整数,且a、b的最大公约数为2.点G和点I分别为△ABC的重心和内心,且∠GIC=90°.求△ABC的周长.