题目内容
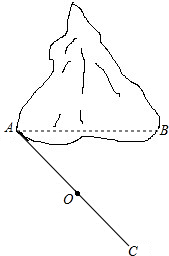 如图,山脚下有A、B两点,用两种方法测量A、B两点间的距离.
如图,山脚下有A、B两点,用两种方法测量A、B两点间的距离.考点:全等三角形的应用
专题:
分析:方法一:作线段AC并取AC的中点O,连接BO并延长至D,使OD=BO,利用“边角边”证明△ABO和△CDO全等,根据全等三角形对应边相等可得AB=CD,然后测量出CD的长,即为AB的长;
方法二:作线段AC并取AC的中点O,连接AC并取中点E,连接OE,测量出OE的长度,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得AB=2OE.
方法二:作线段AC并取AC的中点O,连接AC并取中点E,连接OE,测量出OE的长度,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得AB=2OE.
解答: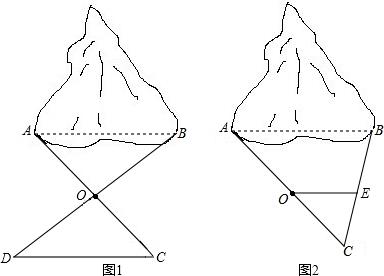 解:方法一,如图1,作线段AC并取AC的中点O,连接BO并延长至D,使OD=BO,
解:方法一,如图1,作线段AC并取AC的中点O,连接BO并延长至D,使OD=BO,
在△ABO和△CDO中,
,
∴△ABO≌△CDO(SAS),
∴AB=CD,
∴测量出CD的长度即为AB的长度;
方法二:如图2,作线段AC并取AC的中点O,连接AC并取中点E,连接OE,
则OE是△ABC的中位线,
所以,AB=2OE,
所以,测量出OE的长,乘以2即为AB的长度.
 解:方法一,如图1,作线段AC并取AC的中点O,连接BO并延长至D,使OD=BO,
解:方法一,如图1,作线段AC并取AC的中点O,连接BO并延长至D,使OD=BO,在△ABO和△CDO中,
|
∴△ABO≌△CDO(SAS),
∴AB=CD,
∴测量出CD的长度即为AB的长度;
方法二:如图2,作线段AC并取AC的中点O,连接AC并取中点E,连接OE,
则OE是△ABC的中位线,
所以,AB=2OE,
所以,测量出OE的长,乘以2即为AB的长度.
点评:本题考查了全等三角形的应用,三角形的中位线平行于第三边并且等于第三边的一半,熟记全等三角形的判定方法和三角形的中位线定理并作出图形是解题的关键.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
下列各题的两项是同类项的是( )
(1)
m2n与
mn2;(2)3ab与-ab;(3)5xyz与5xy;(4)0.4x2yz与0.6x2yz;(5)-3
与5.
(1)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、(1)(2)(3) |
| B、(2)(3)(5) |
| C、(2)(3)(4) |
| D、(2)(4)(5) |
已知:直线y=-
x+
(n为正整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2014=( )
| n |
| n+1 |
| 1 |
| n+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
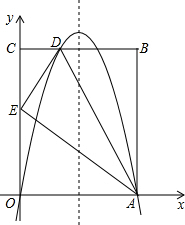 如图,在直角坐标系中,A点在x轴上,AB∥y轴,C点在y轴上,CB∥x轴,点B的坐标为(8,10),点D在BC上,将△ABD沿直线AD翻折,使得点B刚好落在y轴的点E处.
如图,在直角坐标系中,A点在x轴上,AB∥y轴,C点在y轴上,CB∥x轴,点B的坐标为(8,10),点D在BC上,将△ABD沿直线AD翻折,使得点B刚好落在y轴的点E处.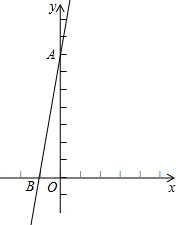 如图,在直角坐标系xOy中,直线y=7x+7交x轴于B,交y轴于A.
如图,在直角坐标系xOy中,直线y=7x+7交x轴于B,交y轴于A.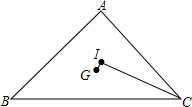 如图,△ABC的三边长BC=a,CA=b,AB=c,a、b、c都是整数,且a、b的最大公约数为2.点G和点I分别为△ABC的重心和内心,且∠GIC=90°.求△ABC的周长.
如图,△ABC的三边长BC=a,CA=b,AB=c,a、b、c都是整数,且a、b的最大公约数为2.点G和点I分别为△ABC的重心和内心,且∠GIC=90°.求△ABC的周长.