题目内容
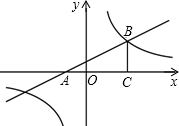 如图,平面直角坐标系中,直线y=
如图,平面直角坐标系中,直线y=| 1 |
| 3 |
| 1 |
| 3 |
| k |
| x |
(1)求双曲线的解析式;
(2)直接写出不等式
| k |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据已知求得B点的横坐标,将横坐标代入直线解析式中求出B点的坐标,把B点坐标代入双曲线y=
即可求得k的值,从而确定出反比例解析式.(2)根据一次函数与反比例函数的两交点的横坐标,以及0,将x轴分为四个范围,找出反比例图象在一次函数图象上方时x的范围即可.
| k |
| x |
解答:解:(1)∵直线y=
x+
与x轴交于点A
∴A(-1,0),OA=1;
∵OC=3AO;
∴OC=3,B点的横坐标为3;
把B点的横坐标为3代入直线y=
x+
中,
解得y=
,
∴B(3,
),
点B在双曲线y=
上,
∴
=
,
解得k=4,
∴双曲线的解析式为:y=
.
(2)解
得x=3或-4;
由图象可知:当0<x<3或x<-4时,满足不等式
>
x+
,
∴不等式
>
x+
的解集为:0<x<3时或x<-4.
| 1 |
| 3 |
| 1 |
| 3 |
∴A(-1,0),OA=1;
∵OC=3AO;
∴OC=3,B点的横坐标为3;
把B点的横坐标为3代入直线y=
| 1 |
| 3 |
| 1 |
| 3 |
解得y=
| 4 |
| 3 |
∴B(3,
| 4 |
| 3 |
点B在双曲线y=
| k |
| x |
∴
| 4 |
| 3 |
| k |
| 3 |
解得k=4,
∴双曲线的解析式为:y=
| 4 |
| x |
(2)解
|
得x=3或-4;
由图象可知:当0<x<3或x<-4时,满足不等式
| k |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
∴不等式
| k |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
点评:此题考查了一次函数与反比例函数的交点问题,利用了待定系数法及数形结合的思想,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知:直线y=-
x+
(n为正整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2014=( )
| n |
| n+1 |
| 1 |
| n+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
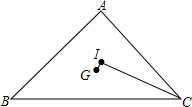 如图,△ABC的三边长BC=a,CA=b,AB=c,a、b、c都是整数,且a、b的最大公约数为2.点G和点I分别为△ABC的重心和内心,且∠GIC=90°.求△ABC的周长.
如图,△ABC的三边长BC=a,CA=b,AB=c,a、b、c都是整数,且a、b的最大公约数为2.点G和点I分别为△ABC的重心和内心,且∠GIC=90°.求△ABC的周长. 如图,已知AB∥CD∥EF,∠BAC=120°,∠CEF=140°,则∠ACE=
如图,已知AB∥CD∥EF,∠BAC=120°,∠CEF=140°,则∠ACE=