题目内容
12.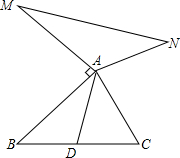 如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.求证:MN=2AD.
如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.求证:MN=2AD.
分析 延长AD至E,使DE=AD,连接BE,根据三角形中线的定义可得BD=CD,然后利用“边角边”证明△BDE和△CDA全等,根据全等三角形对应边相等可得BE=AC=AN,根据全等三角形对应角相等可得∠DBE=∠DCA,再根据内错角相等,两直线平行求出AC∥BE,根据两直线平行,同旁内角互补可得∠ABE+∠BAC=180°,然后求出∠ABE=∠MAN,再利用“边角边”证明△ABE和△MAN全等,根据全等三角形对应边相等可得AE=MN,即可得出答案.
解答 证明:如图,延长AD至E,使DE=AD,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△BDE和△CDA中,
$\left\{\begin{array}{l}{BD=DC}\\{∠BDE=∠ADC}\\{DE=AD}\end{array}\right.$,
∴△BDM≌△CDA(SAS),
∴BE=AC=AN,∠DBE=∠DCA,
∴AC∥BE,
∴∠ABE+∠BAC=180°,
∵∠BAM=∠CAN=90°,
∴∠MAN+∠BAC=180°,
∴∠ABE=∠MAN,
在△ABE和△MAN中,
$\left\{\begin{array}{l}{AB=AM}\\{∠ABE=∠MAN}\\{AN=BE}\end{array}\right.$,
∴△ABE≌△MAN(SAS),
∴AE=AM,
∴MN=2AD.
点评 本题考查了全等三角形的判定与性质,平行线的判定与性质,熟记各性质是解题的关键,难点在于作辅助线构造出全等三角形.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
2. 如图,Rt△ABC中,∠ACB=90°,∠A=35°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的处,则∠ADB1等于( )
如图,Rt△ABC中,∠ACB=90°,∠A=35°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的处,则∠ADB1等于( )
 如图,Rt△ABC中,∠ACB=90°,∠A=35°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的处,则∠ADB1等于( )
如图,Rt△ABC中,∠ACB=90°,∠A=35°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的处,则∠ADB1等于( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
3.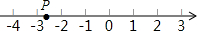 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )
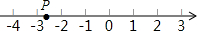 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )| A. | $-\sqrt{10}$ | B. | -3.2 | C. | $\sqrt{7}$ | D. | $-\sqrt{7}$ |
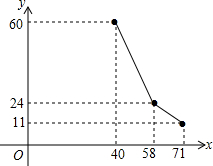 国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x (元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.
国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x (元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.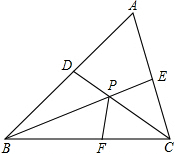 如图,已知△ABC中,∠A=60°,BE,CD分别平分∠ABC,∠ACB,P为BE,CD的交点,求证:BD+CE=BC.
如图,已知△ABC中,∠A=60°,BE,CD分别平分∠ABC,∠ACB,P为BE,CD的交点,求证:BD+CE=BC.