题目内容
5.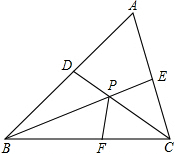 如图,已知△ABC中,∠A=60°,BE,CD分别平分∠ABC,∠ACB,P为BE,CD的交点,求证:BD+CE=BC.
如图,已知△ABC中,∠A=60°,BE,CD分别平分∠ABC,∠ACB,P为BE,CD的交点,求证:BD+CE=BC.
分析 首先结合角平分线的性质结合三角形内角和定理得出∠DPB=∠EPC=60°,∠BPC=120°,再证明△DBP≌△FBP(SAS),进而得出△CEP≌△CFP(ASA),求出EC=FC,进而得出答案.
解答  证明:截取BF=BD,
证明:截取BF=BD,
∵∠A=60°,BE,CD分别平分∠ABC,∠ACB,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=60°,
∴∠DPB=∠EPC=60°,∠BPC=120°,
在△DBP和△FBP中,
$\left\{\begin{array}{l}{BD=BF}\\{∠DBP=∠FBP}\\{BP=BP}\end{array}\right.$,
∴△DBP≌△FBP(SAS),
∴∠DPB=∠BPF=60°,
∴∠CPF=60°,
在△CEP和△CFP中,
$\left\{\begin{array}{l}{∠CEP=∠FCP}\\{PC=CP}\\{∠EPC=∠FPC}\end{array}\right.$,
∴△CEP≌△CFP(ASA),
∴FC=EC,
∴BD+EC=BF+FC,
∴BD+CE=BC.
点评 本题考查了全等三角形的判定以及全等三角形对应边相等的性质,本题中求证△CEP≌△CFP是解题的关键.

练习册系列答案
相关题目
13.若a与b互为相反数,m为正整数,则下列两式计算结果互为相反数的是( )
| A. | am与bm | B. | a2m与b2m | C. | am与-bm | D. | a2m与-b2m |
14.小华想找一个解是2的方程,那么他会选择( )
| A. | 3x+6=0 | B. | $\frac{2}{3}$x=2 | C. | 5-3x=1 | D. | 3(x-1)=x+1 |
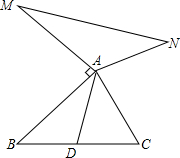 如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.求证:MN=2AD.
如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.求证:MN=2AD.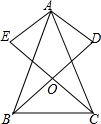 如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O,请说明OB=OC的理由.
如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O,请说明OB=OC的理由.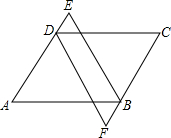 如图,已知AB=CD,AD=BC,DE=BF,说明BE=DF.
如图,已知AB=CD,AD=BC,DE=BF,说明BE=DF.