题目内容
2. 如图,Rt△ABC中,∠ACB=90°,∠A=35°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的处,则∠ADB1等于( )
如图,Rt△ABC中,∠ACB=90°,∠A=35°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的处,则∠ADB1等于( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
分析 根据翻折变换的性质得出∠ACD=∠BCD,∠CDB=∠CDB′,进而利用三角形内角和定理得出∠BDC=∠B′DC,再利用平角的定义,即可得出答案.
解答 解:∵将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,
∴∠ACD=∠BCD,∠CDB=∠CDB′,
∵∠ACB=90°,∠A=35°,
∴∠ACD=∠BCD=45°,∠B=90°-35°=55°,
∴∠BDC=∠B′DC=180°-45°-55°=80°,
∴∠ADB′=180°-80°-80°=20°.
故选C.
点评 此题主要考查了翻折变换的性质以及三角形内角和定理,得出∠BDC和∠B′DC的度数是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若点P是y轴上一动点,则点P到点A(-2,5)和B(-4,3)的距离之和最短时,点P的坐标为( )
| A. | (0,$\frac{8}{3}$) | B. | (0,-$\frac{8}{3}$) | C. | (0,$\frac{13}{3}$) | D. | (0,-$\frac{13}{3}$) |
13.下列四个实数中,无理数是( )
| A. | 1.732 | B. | $\frac{22}{7}$ | C. | $\sqrt{8}$ | D. | 1.$\stackrel{•}{3}$ |
7. 如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1,B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=α,则∠A10B10O=( )
如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1,B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=α,则∠A10B10O=( )
 如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1,B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=α,则∠A10B10O=( )
如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1,B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=α,则∠A10B10O=( )| A. | $\frac{α}{{{2^{10}}}}$ | B. | $\frac{α}{2^9}$ | C. | $\frac{α}{{2{0^{\;}}}}$ | D. | $\frac{α}{18}$ |
 探究一个问题:任意给定一矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形A的周长和面积的一半.
探究一个问题:任意给定一矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形A的周长和面积的一半.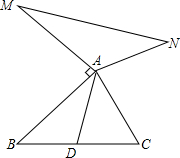 如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.求证:MN=2AD.
如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.求证:MN=2AD.