题目内容
17.求证:(1)对角线互相垂直的平行四边形是菱形;
(2)四条边相等的四边形是菱形.
分析 (1)首先要写已知,求证.接下来根据菱形的定义证明.
(2)同上略.
解答 (1)已知如图1中,四边形ABCD是平行四边形,AC⊥BD,求证:四边形ABCD是菱形.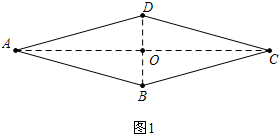
证明:∵四边形ABCD是平行四边形,
∴AO=OC,
∵BD⊥AC,
∴DA=DC(线段的垂直平分线的性质),
∴四边形ABCD是菱形(邻边相等的平行四边形是菱形).
(2)已知如图2中,四边形ABCD中,AB=BC=CD=AC,求证四边形ABCD是菱形.
证明: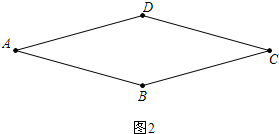 ∵AD=BC,AB=CD
∵AD=BC,AB=CD
∴四边形ABCD是平行四边形(对边相等的四边形是平行四边形),
∵AD=AB,
∴四边形ABCD是菱形(邻边相等的平行四边形是菱形).
点评 本题考查菱形的判定,注意点是文字题目首先要写已知、求证,定理证明必须根据菱形定义去证明,记住菱形的定义是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7. 如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1,B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=α,则∠A10B10O=( )
如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1,B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=α,则∠A10B10O=( )
 如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1,B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=α,则∠A10B10O=( )
如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1,B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=α,则∠A10B10O=( )| A. | $\frac{α}{{{2^{10}}}}$ | B. | $\frac{α}{2^9}$ | C. | $\frac{α}{{2{0^{\;}}}}$ | D. | $\frac{α}{18}$ |
9.能判断四边形ABCD是平行四边形的条件:∠A:∠B:∠C:∠D的值为( )
| A. | 1:2:3:4 | B. | 1:4:2:3 | C. | 1:2:2:1 | D. | 3:2:3:2 |




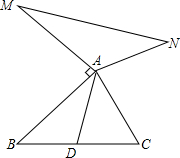 如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.求证:MN=2AD.
如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.求证:MN=2AD.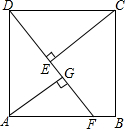 如图,正方形ABCD中,F为AB边上一点,过点A,C分别作DF的垂线,垂足为G和E,若AG=3,EG=1,则BF的长为$\frac{5}{4}$.
如图,正方形ABCD中,F为AB边上一点,过点A,C分别作DF的垂线,垂足为G和E,若AG=3,EG=1,则BF的长为$\frac{5}{4}$.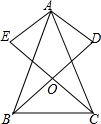 如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O,请说明OB=OC的理由.
如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O,请说明OB=OC的理由.