题目内容
19.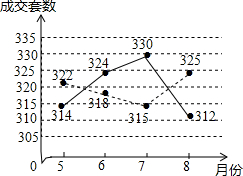 当今社会,住房问题是百姓较为关心的一个话题,某市的相关部门对该市汉江区和新洲区20135-8月的商品住房成交套数进行数据统计,并将汉江区和新洲区所统计的数据绘制车折线统计图(如图所示,图中实线表示的是汉江区的数据,虚线表示的是新洲区的数据).
当今社会,住房问题是百姓较为关心的一个话题,某市的相关部门对该市汉江区和新洲区20135-8月的商品住房成交套数进行数据统计,并将汉江区和新洲区所统计的数据绘制车折线统计图(如图所示,图中实线表示的是汉江区的数据,虚线表示的是新洲区的数据).(1)汉江、新洲两区商品住房成交套数的数据的中位数分别是319、320;
(2)通过计算判断5月到8月,哪个区所销售的商品住房的业绩更稳定?
(3)为了提升两区商品住房的销售业绩,汉江区和新洲区决定联合举行“买房大酬宾”活动,该活动内容为:在汉江区购买A,B或C型的任意一种住房后,再在新洲区购买D,E或F型的任意一种住房时,可享受九折的优惠.小李家正好想在汉江和新洲两区各购买一套住房,请用画树状图法或列表法求出所购买的两套住房恰好是A型和E型的概率.
分析 (1)由中位线的定义,即可求得答案;
(2)首先求得它们的方差,比较方差,即可知哪个区所销售的商品住房的业绩更稳定;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所购买的两套住房恰好是A型和E型的情况,再利用概率公式求解即可求得答案.
解答 解:(1)由折线图可得:汉江、新洲两区商品住房成交套数的数据的中位数分别是319、320;
故答案为:319;320.
(2)汉江区5月到8月的商品住房成交套数的平均数为:$\frac{314+324+330+312}{4}$=320,新洲区的平均数为:$\frac{322+318+315+325}{4}$=320,
汉江区的方差为:$\frac{1}{4}$×[(314-320)2+(324-320)2+(330-320)2+(312-320)2]=54,
新洲区的方差为:$\frac{1}{4}$×[(322-320)2+(318-320)2+(315-320)2+(325-320)2]=14.5,
∴新洲区所销售的商品住房的业绩更稳定.
(3)画树状图得:
∵共有9种等可能的结果,所购买的两套住房恰好是A型和E型的只有1种情况,
∴所购买的两套住房恰好是A型和E型的概率为$\frac{1}{9}$.
点评 此题考查了列表法或树状图法求概率以及方差、中位数的知识.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
10.若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=3cm,BC=5cm,则矩形EFGH的周长是( )
| A. | 16cm | B. | 12cm | C. | 24cm | D. | 36cm |
7. 如图,已知∠1=65°,则∠A与∠C的度数和为( )
如图,已知∠1=65°,则∠A与∠C的度数和为( )
 如图,已知∠1=65°,则∠A与∠C的度数和为( )
如图,已知∠1=65°,则∠A与∠C的度数和为( )| A. | 65° | B. | 115° | C. | 125° | D. | 无法确定 |
14.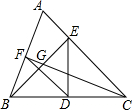 如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )
如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )
 如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )
如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )| A. | 67° | B. | 100° | C. | 113° | D. | 120° |
4.某校安排三辆车,组织八年级学生参加“合肥工业游”活动,其中方圆与吴敏同学都可以从这三辆车中任选一辆搭乘,则方圆与吴敏同车的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
8.随着体育中考的临近,我校随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
则这50名学生这一周在校的体育锻炼时间的众数为8,平均数为6.86小时.
| 时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 4 | 15 | 15 | 16 |
9.王先生准备在儿童节来临之际向母校捐赠一批(大于100条)某种品牌的跳绳,采购跳绳有在实体店和网店购买两种方式,通过洽谈,获得了以下信息:
(1)请分别写出王先生用这两种方式购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式;
(2)王先生选取哪种方式购买跳绳省钱?
(3)王先生准备用不超过10000元购买跳绳,他最多能购买多少条跳绳?
| 购买方式 | 标价(元/条) | 优惠条件 |
| 实体店 | 40 | 全部按标价的8折出售 |
| 网店 | 40 | 购买100或100条以下,按标价出售; 购买100条以上,从101条开始按标价的7折出售(免邮寄费) |
(2)王先生选取哪种方式购买跳绳省钱?
(3)王先生准备用不超过10000元购买跳绳,他最多能购买多少条跳绳?
 如图,MN是半径为4cm的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为4$\sqrt{2}$.
如图,MN是半径为4cm的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为4$\sqrt{2}$.