题目内容
9.王先生准备在儿童节来临之际向母校捐赠一批(大于100条)某种品牌的跳绳,采购跳绳有在实体店和网店购买两种方式,通过洽谈,获得了以下信息:| 购买方式 | 标价(元/条) | 优惠条件 |
| 实体店 | 40 | 全部按标价的8折出售 |
| 网店 | 40 | 购买100或100条以下,按标价出售; 购买100条以上,从101条开始按标价的7折出售(免邮寄费) |
(2)王先生选取哪种方式购买跳绳省钱?
(3)王先生准备用不超过10000元购买跳绳,他最多能购买多少条跳绳?
分析 (1)根据题意和表格可以求得王先生用这两种方式购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式;
(2)将第一问中求得的两个函数,令它们相等,即可求得x的值,从而可以得到王先生选取哪种方式购买跳绳省钱;
(3)令y=10000,可以求得两种方式分别可以购买的跳绳数,从而可以得到王先生准备用不超过10000元购买跳绳,他最多能购买多少条跳绳.
解答 解:(1)由题意可得,
王先生在实体店购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式为:y=40x×0.8=32x;
王先生在网店购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式为:y=40×100+(x-100)×40×0.7=28x+1200;
即王先生在实体店购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式为:y=32x;
王先生在网店购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式为:y=28x+1200;
(2)∵32x=28x+1200,
解得,x=300
∴当100<x<300时,在实体店购买省钱,
当x=300时,在实体店和网店购买一样,
当x>300时,在网店购买省钱;
(3)将y=10000代入y=32x,得x=312.5≈312
将y=10000代入y=28x+1200,得x≈314
即王先生准备用不超过10000元购买跳绳,他最多能购买314条跳绳.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,列出相应的函数关系式,会根据函数的值,求相应的x的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列关于方程x2+x-1=0的说法中正确的是( )
| A. | 该方程有两个相等的实数根 | |
| B. | 该方程有两个不相等的实数根,且它们互为相反数 | |
| C. | 该方程有一根为$\frac{{1+\sqrt{5}}}{2}$ | |
| D. | 该方程有一根恰为黄金比例 |
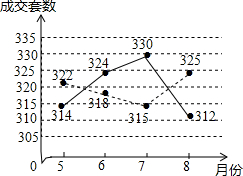 当今社会,住房问题是百姓较为关心的一个话题,某市的相关部门对该市汉江区和新洲区20135-8月的商品住房成交套数进行数据统计,并将汉江区和新洲区所统计的数据绘制车折线统计图(如图所示,图中实线表示的是汉江区的数据,虚线表示的是新洲区的数据).
当今社会,住房问题是百姓较为关心的一个话题,某市的相关部门对该市汉江区和新洲区20135-8月的商品住房成交套数进行数据统计,并将汉江区和新洲区所统计的数据绘制车折线统计图(如图所示,图中实线表示的是汉江区的数据,虚线表示的是新洲区的数据).